Parts of Quadratics
Basic Quadratic Equations
Graphing a Parabola
Formulas
BONUS QUESTIONS
100
Define vertex
The vertex is a point in which the parabola reaches its maximum or minimum height - the turning point
100
What are the forms a quadratic is written in?
1) Standard Form
2) Vertex Form
3) Intercept Form
100
What are some of the key parts of a parabola (give at least 3)
Maximum, minimum, vertex, zeros, axis of symmetry, x-intercept, y-intercept
100
What is intercept form of a quadratic?
f(x) = a (x-p) (x-q)
100
Without knowing the equation how can you tell if a parabola is positive or negative just by looking at the graph?
If its curving up and is resembling a happy face the parabola would be positive:
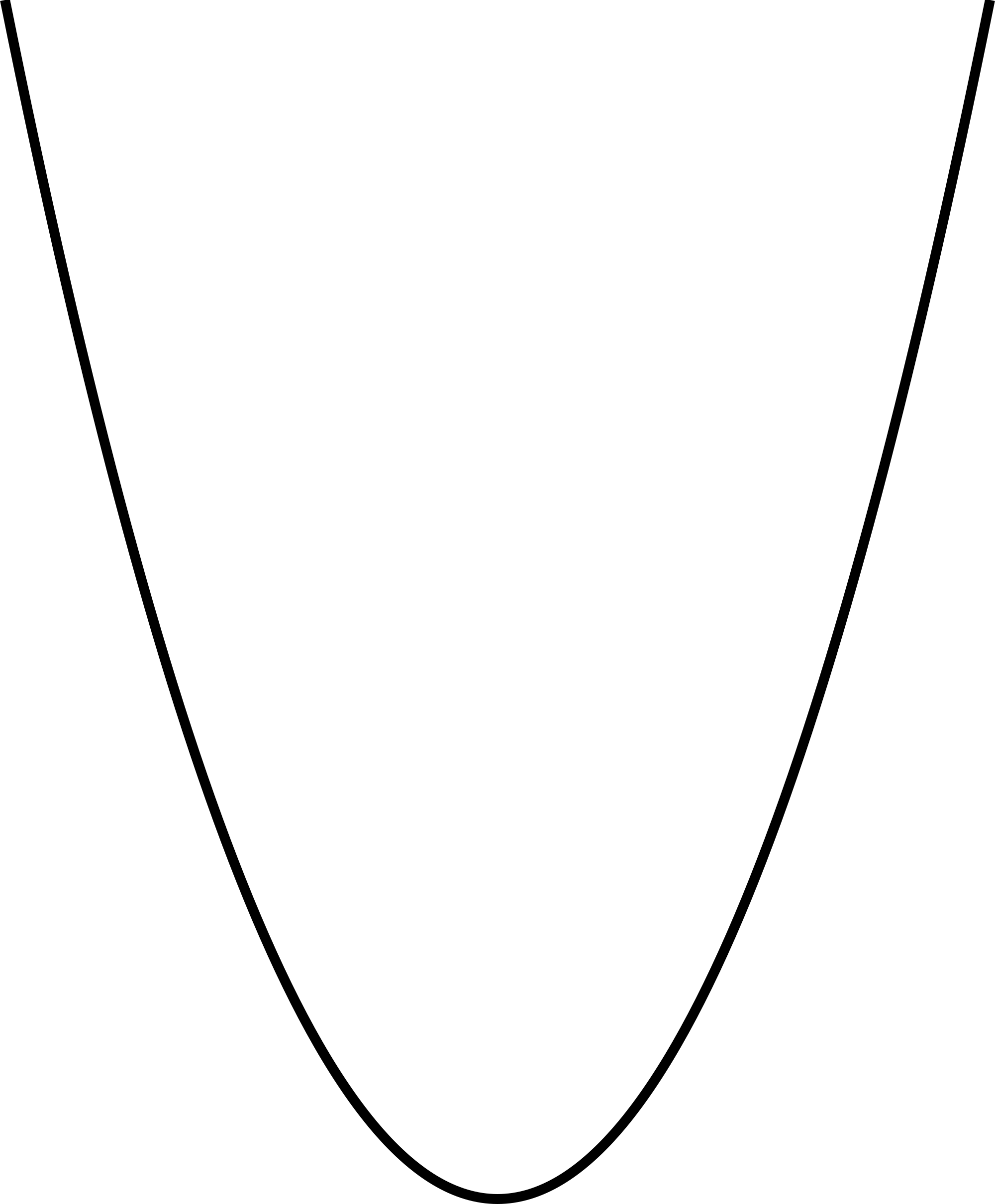
And if the curve is the opposite of this, curving downwards and resembling a sad face it would be negative
* way to remember: sad is a negative feeling
happy is a positive feeling
200
The y-coordinate of the vertex is called the...
maximum or minimum value
200
Which form is represented by the equation ax^2+bx+c
Standard form
200
How do you graph a parabola from vertex form?
y = 2 (x-2)2 + 18
You will start at the at the vertex (2, 18) then create a table of values to graph
200
What is the domain of all parabolas?
all real numbers
200
State the vertex, zeros, maximum/minimum value, and whether the parabola is positive or negative (the direction of opening)
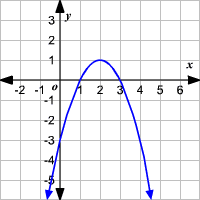
Vertex: (2,1)
Zeros: 1 and 3
maximum value: 1
Direction of opening: down
300
Define the axis of symmetry
The axis of symmetry is is parallel to the y-axis and it passes through the vertex; in other words it divides the parabola in half.
300
The vertex form equation
f(x) = a (x-h)2 + k
300
How do you graph a parabola from intercept form?
y = -2 (x+2) (x+6)
since you have the zeros -2 and -6 you can now find the axis of symmetry by adding the two zeros and dividing that answer by two
then sub that answer ... x=4 into the equation and solve for y then giving you the vertex.
next plot the zeros vertex to graph
300
What is the range of y = - (x-2)2 - 4?
y is less than or equal to -4
from negative infinity to -4
300
If you don't have a graph just an equation how can you determine the direction of opening?
If the value of a is negative, then the parabola will be opening downwards. If positive, upwards.
400
How do you determine if a parabola is going to have a maximum or minimum?
If the parabola opens upward, it is a minimum. If it opens downward, it is a maximum.
400
What forms are the equations given below written in
1) Y=2(x-3)2+62
2) Y=4x2+6x+10
1) Vertex form
2) Standard form
400
What does the a value tell us?
It tells us if the parabola is going to open upward or downward
400
What is the formula for the axis of symmetry when given a function in intercept form?
x = (p+q)/2
400
What is the formula for the axis of symmetry when given a function in standard form?
x = -b/2a
500
State the zeros in the given graph below.
The zeros are -2 and +2
500
Write an equation of a parabola that opens up and has a vertex of (-4,9)
y = a(x+4)2 + 9
500
Identify the vertex from the graph? How many zeros doe the quadratic have? Is a positive or negative?
vertex: (-2,5)
2 zeroes
a is negative
500
If you have found the axis of symmetry, how do you find the vertex?
Plug the axis of symmetry in for x to get y. These are the x and y coordinates of the vertex (x, y)
500
Do the equations listed below represent a quadratic? Why or why not, explain.
1) y=2x+3
2) y=2(x-5)(x+6)
1) This equation does not as it is in y=mx+b form which would create a line not a quadratic
2) This equation does because it is in intercept form therefore it creates a parabola