Parallel Lines
Parallel Lines and Transversals
Special Angle Relationships
Proving Lines Parallel
Linear Pairs/Vertical Angles
100
Sometimes, always, or never?
Skew lines ______ intersect.
Never
100
If two parallel lines are cut by a transversal, what is the relationship between the consecutive interior angles formed?
Consecutive interior angles add up to 180.
100
If two parallel lines are cut by a transversal, what is the relationship between the corresponding angles formed?
Corresponding angles are congruent.
100
Two lines are cut by a transversal. If angles A and B are corresponding and the measure of angle A is 80 degrees and the measure of angle B is 90, does that prove that the lines are parallel? Why?
No. Angles A and B must be congruent.
100
Fill in the blank:
Vertical angles are ______
Linear pairs are _______
Congruent
Supplementary
200
Sometimes, always, or never?
Skew lines are _________ parallel.
Never
200
If two parallel lines are cut by a transversal, what is the relationship between the alternate interior angles formed?
Alternate interior angles are congruent.
200
If two lines are parallel and cut by a transversal, then consecutive interior angles are _____________.
Name and angle measure.
Supplementary, 180 degrees
200
Two lines are cut by a transversal. If angles A and B are consecutive interior angles and the measure of angle A is 80 degrees and the measure of angle B is 100, does that prove that the lines are parallel? Why? What theorem was used?
Yes. Consecutive interior angles add up to 180 degrees using Consecutive Interior converse.
200
What is the value for x in the diagram. Explain what angle relationship you used.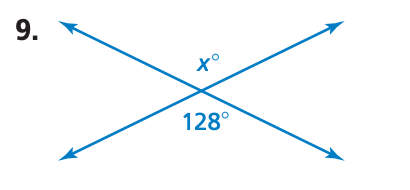 
128 degrees, because they are vertical angles which are always congruent
300
Sometimes, always, or never?
Two parallel lines __________ lie in the same plane.
Always
300
If two parallel lines are cut by a transversal, what is the relationship between the vertical angles formed?
Vertical angles are congruent.
300
If two parallel lines are cut by a transversal, and alternate interior angles are congruent, and if one of those alternate interior angles is x+15, and the other is 2x+5.
What is the value of x?
x = 10
300
Two lines are cut by a transversal. If angles A and B are alternate interior angles and the measure of angle A is 80 degrees and the measure of angle B is 100, does that prove that the lines are parallel? Why? What theorem was used?
No. Alternate interior angles are congruent. Alternate interior Converse was not upheld.
300
Find the value of x and explain what angle relationship you used to reach your answer.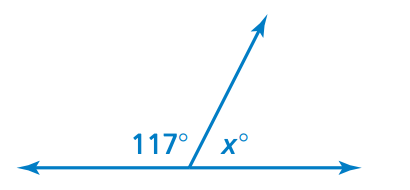
x = 63
400
Define skew lines
Two lines that will never intersect that are on different planes.
400
If two parallel lines are cut by a transversal, what is the relationship between the alternate exterior angles formed?
Alternate exterior angles are congruent.
400
If two parallel lines are cut by a transversal, then consecutive interior angles are supplementary, and if one of those consecutive interior angles is 3x+4 and the other is 2x+6,
Find the value of x
x=34
400
Two lines are cut by a transversal. If angles A and B are consecutive exterior angles and the measure of angle A is 80 degrees and the measure of angle B is 80, does that prove that the lines are parallel? Why? Draw a picture and describe the theorems used.
No. Same side exterior angles must be supplementary.
400
Solve for x: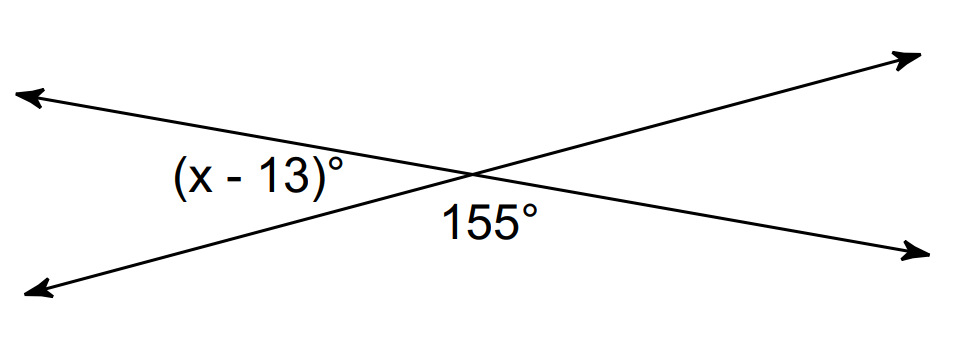 
x = 38
500
Describe a real-world example or model of parallel planes.
Ex: floor and ceiling
500
Two parallel lines are cut by a transversal. If Angles 3 and 4 are alternate exterior angles and the measure of angle 3 is 80 degrees, what is the mesure of angle 4?
80 degrees
500
If two lines are parallel and cut by a transversal, then consecutive interior angles are supplementary, and if one of those interior angles is 7x+12 and the other is 3x+8...
What are the measures of each angle?
56 degrees and 124 degrees
500
Two lines are cut by a transversal. If angles A and B are vertical angles and are congruent, does that prove that the lines are parallel? Why?
No. Vertical angles are always congruent and therefor do not prove lines are parallel.
500
Solve for x: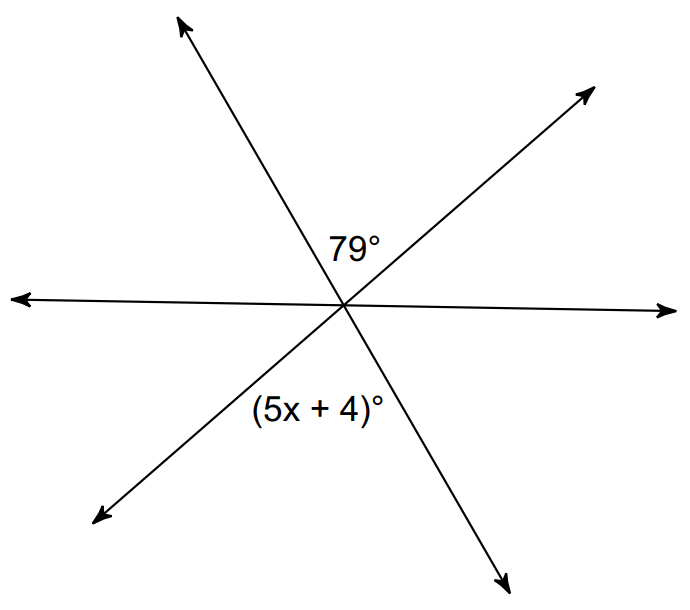 
x = 15