Angle Pairs
Are the lines parallel?
Solve for x.
Congruent / Supplementary
Are the lines parallel or perpendicular or neither?
100
∠5 and ∠7? 
Linear Pair
100
<4 and <6 are corresponding angles that are found after two lines are cut by a transversal. The measure of both these angles is 126 degrees. Are the lines parallel?
Yes. Corresponding Angles are congruent only when lines are parallel.
100
Find the value of x, which angle pair, and write the equation?
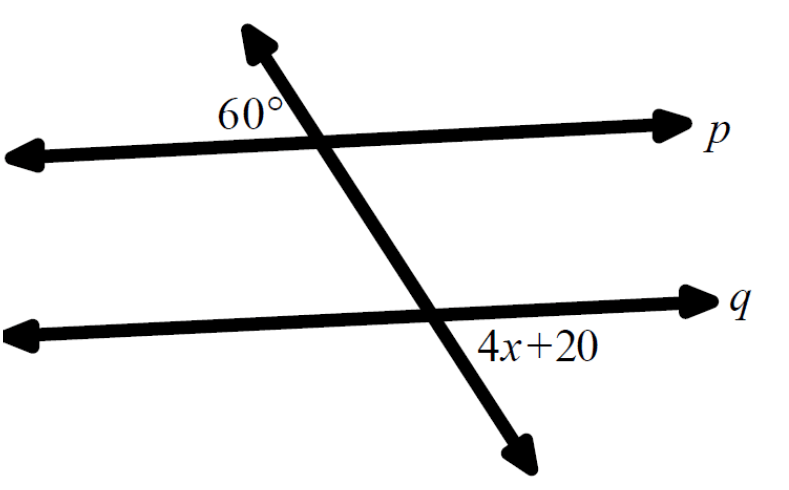
x = 10, Alternate Exterior Angles, 60 = 4x + 20
100
Identify if the angles are congruent or supplementary, and write the equation to solve.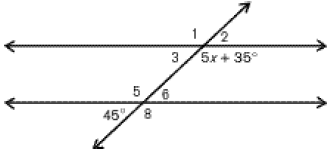 
Supplementary, 5x + 35 + 45 = 180
100
Determine if the two lines are parallel, perpendicular, or neither:
y = 5x +12
10x - 2y = -6
parallel
2nd equation written in slope-intercept form
y = 5x + 3
200
∠5 and ∠4
Alternate Interior Angles
200
<7 and <8 are a same-side interior angles that are found after two lines are cut by a transversal. The angles are supplementary Are the lines parallel?
Yes, same-side interior angles add to 180 only when lines are parallel.
200
Find the value of x, which angle pair, and write the equation?
x = 5, Corresponding Angles, 10x + 4 = 54
200
Identify if the angles are congruent or supplementary, and write the equation to solve.
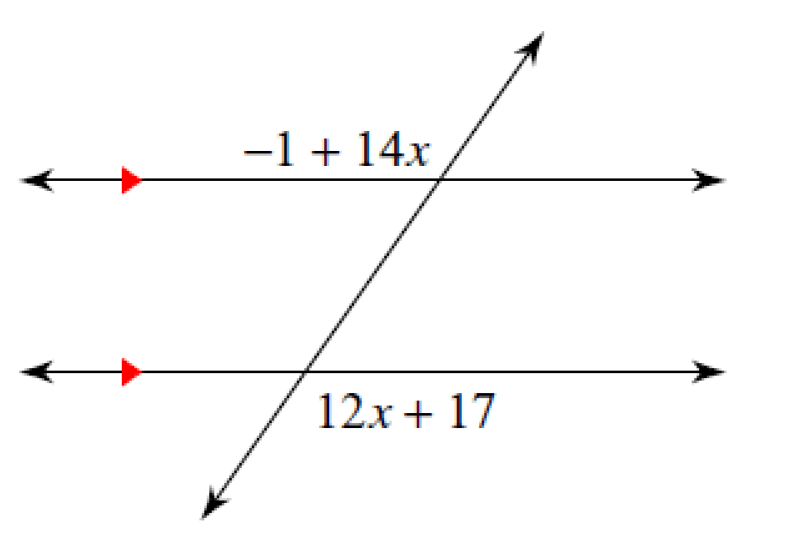
Congruent, -1 + 14x = 12x + 17
200
Determine if the two lines are parallel, perpendicular, or neither:
y = (3/7)x - 5
y = -(7/3) +21
Perpendicular
negative reciprocal slopes
300
∠6 and ∠3
Alternate Interior Angles
300
<2 and <9 are alternate exterior angles that are found after two lines are cut by a transversal. The measure of <2 = 100 and the measure of <9 = 99. Are the lines parallel?
No, lines are only parallel when alternate exterior angles are congruent.
300
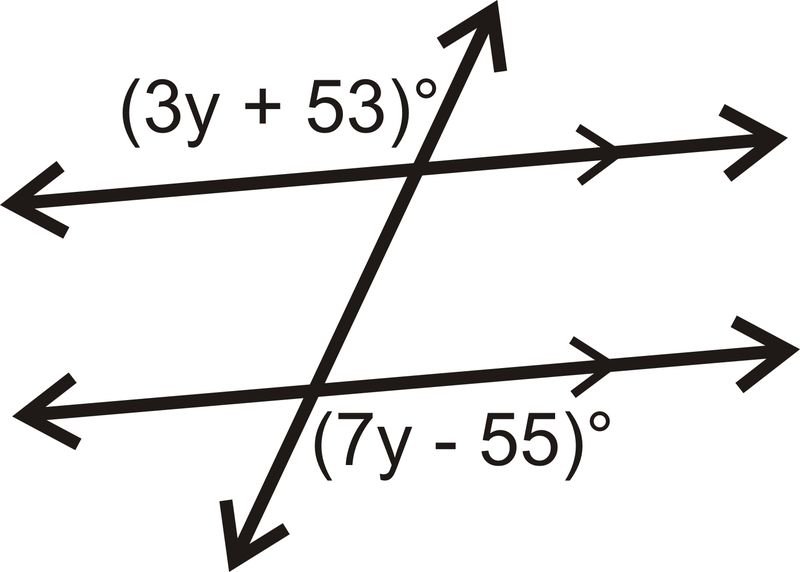
Find the value of y, which angle pair, and write the equation?
Y= 27, Alternate Exterior Angles, 3y + 53 = 7y - 55
300
Identify if the angles are congruent or supplementary, and write the equation to solve. 
Supplementary, 3x - 10 + 5x + 30 = 180
300
Determine if the two lines are parallel, perpendicular, or neither:
15x + 19y = 21
3x + 26y = 28
Neither
1st line: y = -(15/19)x + (21/19)
2nd line: y = -(3/26)x + (28/26)
400
∠1 and ∠8
Alternate Exterior Angles
400
<3 and <5 are consecutive interior angles that are found after two lines are cut by a transversal. The measure of <3 is 60 degrees and the measure of <5 is 120 degrees. Are the lines parallel?
Yes, consecutive interior angles add up to 180 only when lines are parallel.
400
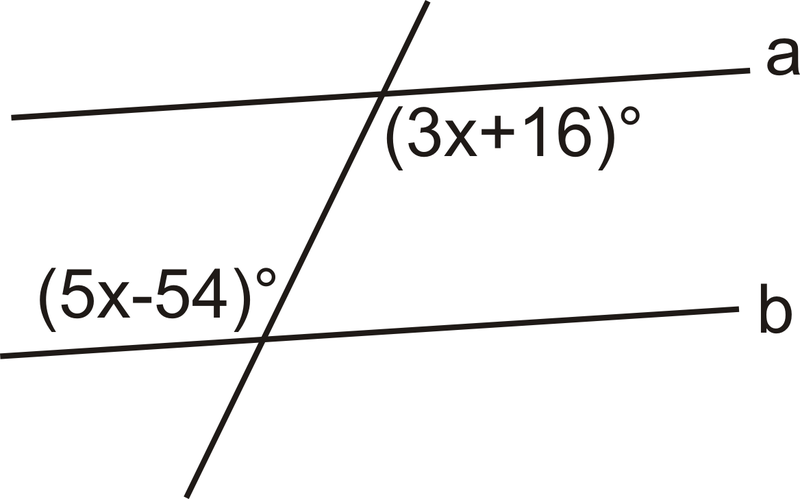
Find the value of x, which angle pair, and write the equation?
X= 35, Alternate Interior Angle, 3x + 16 = 5x -54
400
Identify if the angles are congruent or supplementary, and write the equation to solve. (If solving for x)
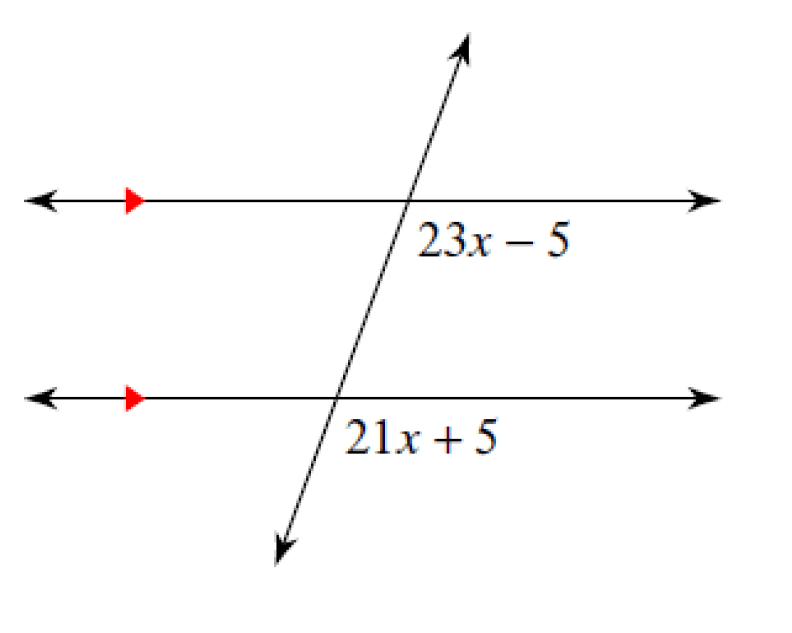
Congruent, 21x + 5 = 23x - 5
400
Find the slopes of both lines to determine if the lines are parallel, perpendicular, or neither:
Line 1: (0, 3) (3, 1)
Line 2: (-1, 4) (-7, -5)
perpendicular
Line 1 Slope is -(2/3)
Line 2 Slope is (3/2)
500
∠3 and∠5
Same Side Interior Angles
500
<3 and <5 are consecutive interior angles that are found after two lines are cut by a transversal. The measure of <3 is 59 degrees and the measure of <5 is 131 degrees. Are the lines parallel?
No, lines are parallel only when consecutive interior angles add to 180. <3 and <5 add to 190.
500
Find the value of x, which angle pair, and write the equation?
X=35, Same Side Interior, 2x + 43 + 2x - 3 = 180
500
Identify if the angles are congruent or supplementary, and write the equation to solve. (If solving for x)
Supplementary, x + 109 + x + 89 = 180
500
Find the slopes of both lines to determine if the lines are parallel, perpendicular, or neither:
Line 1: (2, -1) (5, -7)
Line 2: (0, 0) (-1, 2)
parallel
Line 1 Slope is -2
Line 2 Slope is -2