Graphing and Analyzing Polynomial Functions
Polynomial Functions Operations
Factoring and Solving Polynomial Equations
The Fundamental Theorem of Algebra
Transformations of Polynomial Functions
100
Decide whether the function is a polynomial function.
f(x) = 9x^4 + 8x^3 - 6x^-2 + 2x
The function is not a polynomial function.
100
Find the sum.
(3x^2 + 4x - 1) + (-2x^2 - 3x + 2)
x^2 + x + 1
100
Factor the polynomial completely.
10w^10-19w^9+6w^8
w^8(5w-2)(2w-3)
100
Identify the number of solutions or zeros.
h(x)=5x^4+7x^8-x^12
12
100
Describe the transformation of f represented by g.
f(x)=x^5,g(x)=(x-2)^5-1
The graph of g is a translation 2 units right and 1 unit down of the graph of f.
200
Write the polynomial function in standard form and state its degree, type, and leading coefficient.
g(x) = sqrt(3) - 12x + 13x^2
Degree: 2
Type: Quadratic
Leading coefficient: 13
Standard form:
g(x) = 13x^2 - 12x + sqrt(3)
200
Find the difference.
(3x^3 - 2x^2 + 4x - 8) - (5x^3 + 12x^2 - 3x - 4)
-2x^3 - 14x^2 + 7x - 4
200
Factor the polynomial completely.
16t^7+250t^4
2t^4(2t+5)(4t^2-10t+25)
200
Find all zeros of the polynomial function.
h(x)=x^3+5x^2-4x-20
-5, -2, and 2
200
Describe the transformation of f represented by g.
f(x)=x^6, g(x)=-3x^6
The graph of g is a vertical stretch by a factor of 3 followed by a reflection in the x-axis of the graph of f.
300
Describe the end behavior of the graph of the function.
f(x) = 11 - 18x^2 - 5x^5 - 12x^4 - 2x
300
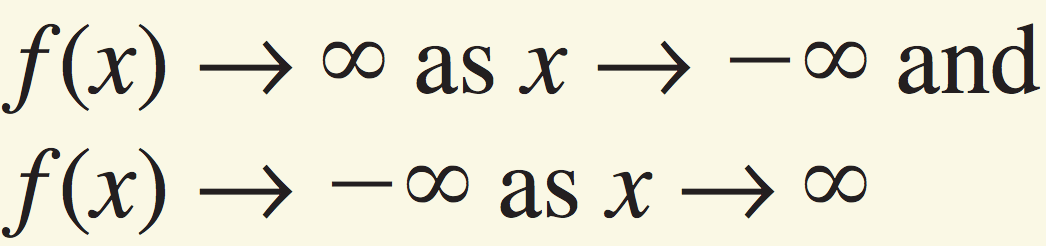
Find the product.
(-x-3)(2x^2+5x+8)
-2x^3-11x^2-23x-24
300
Determine whether the binomial is a factor of the polynomial.
t(x)=48x^4+36x^3-138x^2-36x; x+2
The binomial is a factor of the polynomial.
300
Determine the number of imaginary zeros for the function with the given degree and graph.
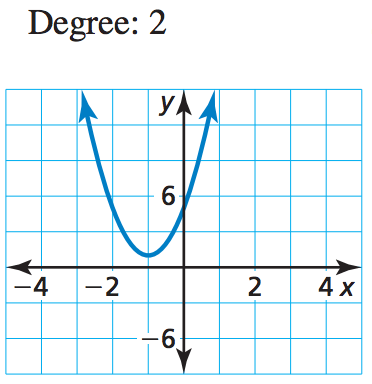
2
300
Write a rule for g that represents the indicated transformations of the graph of f.
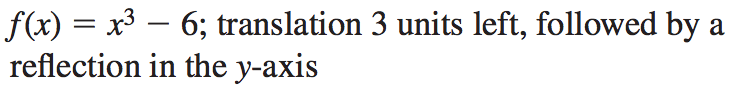
g(x)=-x^3+9x^2-27x+21
400
Determine whether the function is even, odd, or neither.
h(x) = x^5 + 3x^4
The function is neither.
400
Divide using synthetic division.
(x^4+4x^3+16x-35) divide (x+5)
x^3-x^2+5x-9+frac10(x+5)
400
Solve the equation.
12n^2+48n=-n^3-64
n=-4
400
Determine the possible numbers of positive real zeros, negative real zeros, and imaginary zeros for the function.
g(x)=x^4-x^2-6
400
Write a rule for g that represents the indicated transformations of the graph of f.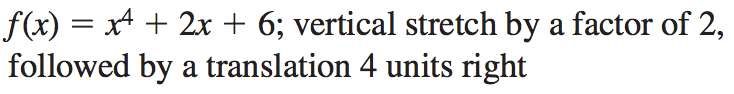 
g(x)=2x^4-32x^3+192x^2-508x+508
500
Find all real zeros of the function.
g(x)=4x^3+x^2-51x+36
-4, frac3(4), and 3
500
Divide using polynomial long division.
(3x^2-14x-5) divide(x-5)
3x+1
500
Find all the real zeros of the function.
f(x)=x^3-14x^2+55x-42
1, 6,and 7
500
Write a polynomial function f of least degree that has rational coefficients, a leading coefficient of 1, and the given zeros.
3i,2-i
f(x)=x^4-4x^3+14x^2-36x+45
500
Write a rule for g that represents the indicated transformations of the graph of f.
g(x)=-27x^3-18x^2+7