Polynomial Division
Polynomial Theorems
Graphing Polynomials
100
(x^3+2x^2-10x-5)\div(x+5)
x^2-3x+5-30/(x+5)
100
If the remainder after division equals zero, what does that mean for the divisor?
The divisor is a factor of the dividend?
100
A zero with a multiplicity of 2 will do what on the x-axis?
Bounce or touch the graph and turn around.
200
(5x^5-4x^4+3x^3-2x^2+x+1)\div (x-1)
5x^4+x^3+4x^2+2x+3+4/(x-1)
200
Find f(2) for
f(x)=2x^2 +3x-34
-20
200
What is the degree of the polynomial:
f(x)=2x^2-10x+4x^3-12x^4+1
Degree= 4
300
(x^3-2x^2-4)div(x-3)
x^2+x+3+5/(x-3)
300
What is the remainder when you divide
(2x^3-5x^2+6x-12)div(x-4)
60
300
Find all zeros and multiplicities of the following:
f(x)=x^3+2x^2+x
x=0 M1
x=-1 M2
400
(3x^4+x^3-17x^2+19x-6)\div(x^2-2x+1)
3x^2+7x-6
400
What are all the possible rational zeros of the polynomial:
f(x)=2x^3-4x^2+12x-8
+-1, +-1/2, +-2, +-4,+-8
400
Write out the end behavior for the graph of:
f(x)=-3x^4-3x^2+12x
x->-oo, f(x)->-oo
x->oo, f(x)->-oo
500
(2x^3-5x^2+x-10)div(x^2-4x+1)
2x+3+(11x-13)/(x^2-4x+1)
500
Find all zeros of the polynomial:
x^3+2x^2-5x-6
x=2, -3, -1
500
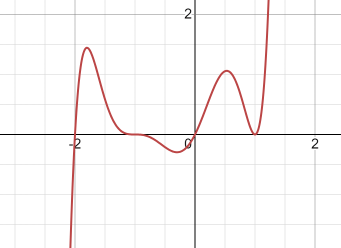
Graph the following polynomial:
f(x)=x(x+2)(x-1)^(2)(x+1)
