What's your function?
Opposites Attract
Sub-Zero
House Divided
Inside-Out
100
Consider the following functions....
what is (f-g)(x)?
f(x)=3x^2-4x
g(x)=7x^2+x
-4x^2-5x
100
Find the inverse of
g(x)=-4x+3
g^-1(x)=(x-3)/-4
100
Consider the following functions....what is (g(f(2))?
f(x)=8x-7
g(x)=x^2
81
100
Use long division to divide
(2x^3+2) div (x+3)
2x^2-6x+18+(-52)/(x+3)
100
Find
f(g(4))
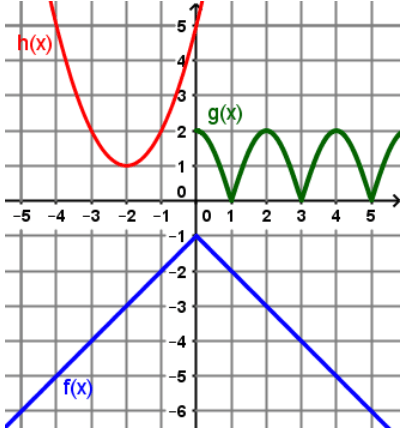
-3
200
Consider the following functions....
what is (f*g)(x)?
f(x)=x-4
g(x)=7x^2+x
7x^3-27x^2-4x
200
When we find the inverse of a function, what does the word INVERSE mean?
Switch x & y
200
Consider the following functions....what is (f(g(x))?
f(x)=16x+1
g(x)=x-1
16x-15
200
Divide the following polynomials:
(x^3-2x^2-4) div (x-2)
x^2+2x+2
200
Find
f(h(-4))
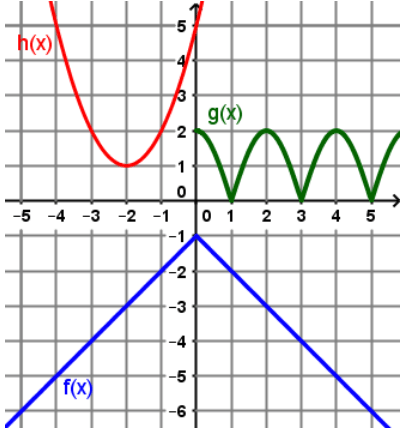
-6
300
Consider the following functions....
what is (f+g)(x)?
f(x)=3x^2-4x
g(x)=11x+13
3x^2+7x+13
300
What is the inverse of the following relation...
(2,-3), (1,8), (-5,-7), (9,1)
(-3,2), (8,1), (-7,-5), (1,9)
300
When using composition (or substitution), how should you work the problem?
First do the Inside, then the Outside
300
Use synthetic division to divide:
(6x^3-2x^2+5x+3)/(x+3)
6x^2-20x+65+(-195)/(x+3)
300
Find
(h(f(3))
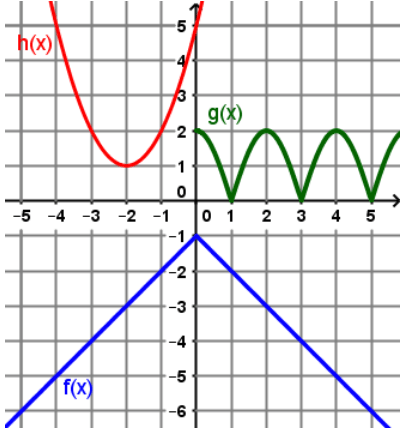
5
400
Consider the following functions....
what is (f-g)(3)?
f(x)=3x^2-4x
g(x)=7x^2+x
-51
400
Find the inverse of
f(x)=(9-x)/12
f^-1(x)=-(12x-9)
400
Consider the following functions....what is (g(f(x))?
f(x)=x-7
g(x)=x^2+3
x^2-14x+52
400
What is the remainder when
(3x^2+5x+10) div (x-5)
110
400
Find
(g(h(0))
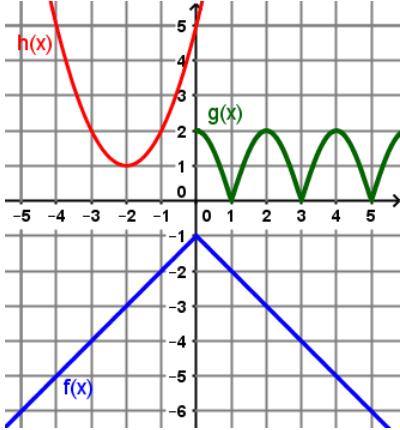
0
500
Consider the following functions....
what is (f/g)(2)?
f(x)=x^2-4
g(x)=6x-11
0
500
Find the inverse of
h(x)=x^2+9
h^-1(x)=sqrt(x-9)
500
Consider the following functions....what is (f(g(4))?
f(x)=16x+1
g(x)=x-1
49
500
Divide the following:
(x^3+5)/(x-1)
x^2+x+1+(6)/(x-1)
500
Find
g(g(1))
2