How do you identify the terms in a polynomial expression?
they are separated my + or -
The degree of this polynomial:
x3 - 7x2 + 4x5 - 19x7
7
Add the Polynomials
(4x + 9) +(x - 4)
5x + 5
Subtract the polynomials:
(g - 4) - (3g - 6)
-2g + 2
3(3x)
9x
(x + 6) (x + 3)
x2 +9x +18
Find the Perimeter
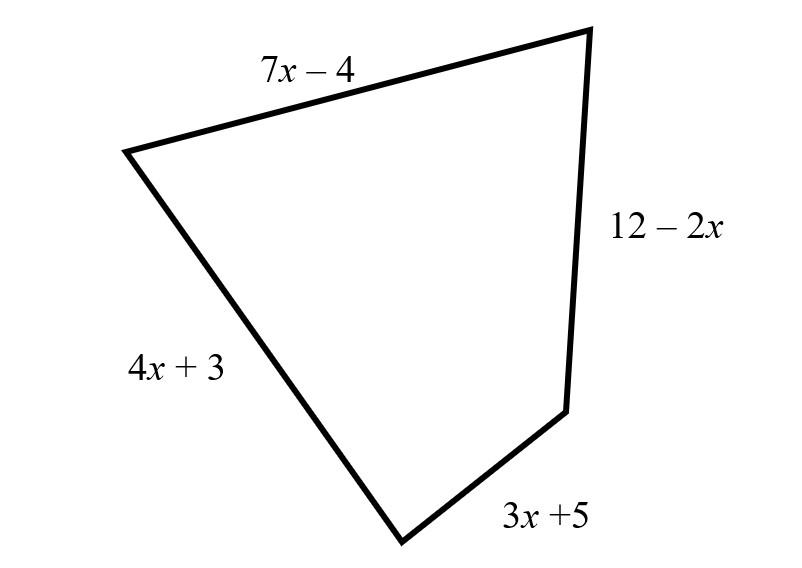
12x + 16
DAILY DOUBLE
The number before a variable within a term is called the...
Coefficient
Classify by its degree and number of terms:
10x
Linear Monomial
Add the polynomials:
(-3a - 2) + (7a + 5)
4a + 3
Subtract the polynomials:
(-5h - 2) - (7h +6)
-12h - 8
Multiply the Polynomials:
(3x)(2y)
6xy
(3x - 4)(2x + 5)
6x2 + 7x - 20
A square has an area of 20.25 in2. Find the length of one side.
4.5 in.
What is the other word we can use to describe an exponent?
Power
A constant polynomial has a degree of this.
0
Add the polynomials:
(x2 +3x + 5) + ( -x2 +6x)
9x + 5
Subtract the polynomials:
(-x2 - 5) - (-3x2 -x -8)
2x2 + x +3
Multiply the Polynomials:
3x2 (2x4 + 4)
6x6 + 12x2
(x - 8)(2x + 3)
2x2 - 13x - 24
Find the area of the rectangle
5x2 + 42x + 16
The sum of the exponents on the variables in each term is__________, and the highest of these is the _____________.
Degree of the term
Polynomial degree
Rewrite this polynomial in standard form
-6a4 + 10a3 + 14a7 - 22a2 + 33
14a7 - 6a4 + 10a3 -22a2 +33
Add the polynomials:
(t2 + 3t3 -3) + (2t2 +7t -2t3)
t3 +3t2 +7t -3
Subtract the Polynomials:
(k2 + 6k3 -4) - (5k3 + 7k -3k2)
k3 + 4k2 -7k -4
-4x(x-2)
-4x^2 + 8x
(y + 9)2
y2 + 18y + 81
A rectangle has a length which is twice the width. The area of the rectangle is 242 cm2. Find the length and width.
l = 22
w = 11
Terms that have the same variables and the same degree are....
Like terms
Refers to the highest exponent in a polynomial, or the exponent on a specific term
Degree
Add the polynomials:
(-1 + x2 + 2x) + (1 -2x + 2x2)
3x2
Subtract the Polynomials:
(2x2 - 3x) - (x2 -2x + 4)
x2 - x - 4
(2x-3y+6)(3y)
6xy-9y2+18y
(x - 12)(x + 12)
x2 - 144
Find the area of the triangle as a simplified polynomial:
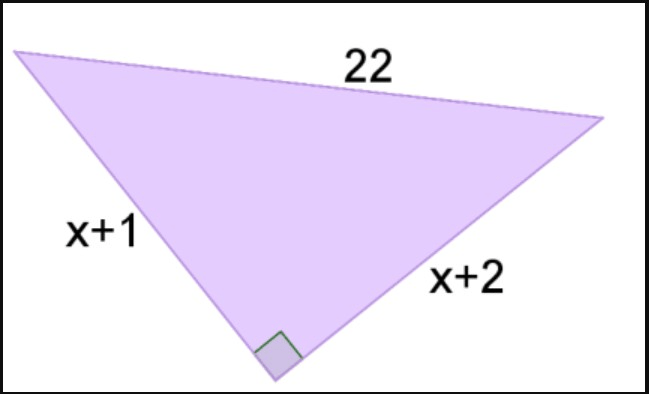
A = 0.5x2 + 1.5x + 1