Basics
Basics
& Multiplicity
Polynomials
Characteristics
Identify the degree and leading term of the following polynomials:
1) f(x) = 6x2 + 8x3 - 5x4 - 3x + 23
2) g(x) = 2(x + 5)(x - 7)2
1) Degree = 4, LT = -5x4
2) Degree = 3, LT = 2x3
Determine the end behavior of the following function. Use proper notation.
f(x) = 4x3 - 8x2 + 3x4 + x - 10
`As ` x ->-\infty, f(x) ->\infty
`As ` x ->\infty, f(x) ->\infty
We know that x = -4 is a root of g(x) = x3 - 5x2 - 22x + 56. Use this information to write g(x) in factored form.
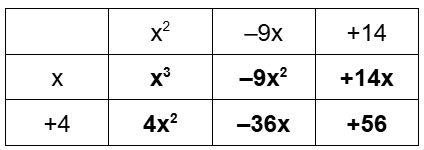
g(x) = (x + 4)(x2 - 9x + 14)
g(x) = (x + 4)(x - 2)(x - 7)
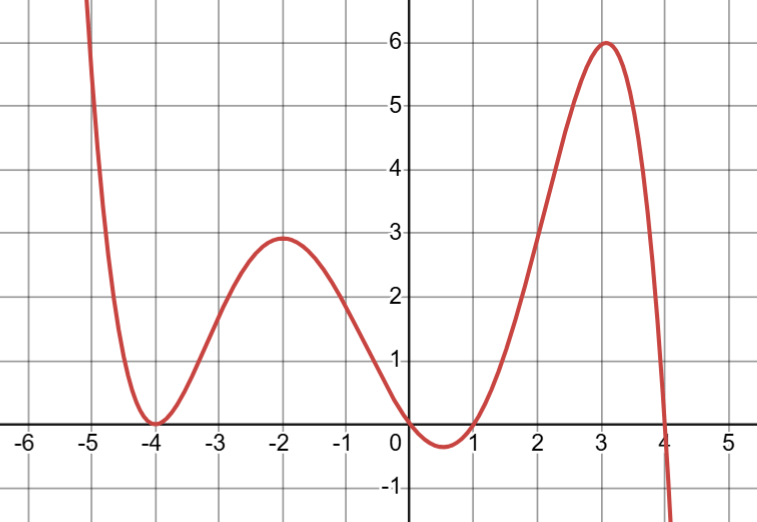
Identify the x & y intercepts
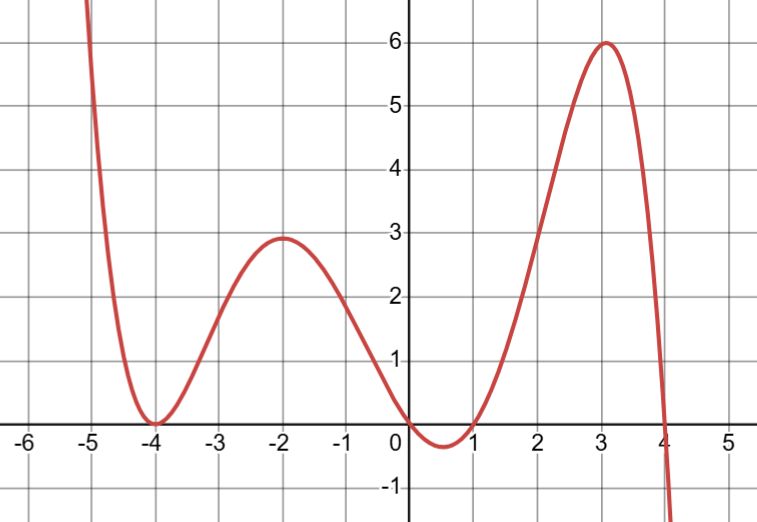
X-int: (-4, 0), (0, 0), (1, 0), (4, 0)
Y-int: (0, 0)
We are given the following polynomials:
f(x) = 4x2 - 5x3 + x - 7
g(x) = 7x4 + 2x3 - 8x - 1
Find t(x) = f(x) - g(x) and write you answer in standard form.
t(x) = (-5x3 + 4x2 + x - 7) - (7x4 + 2x3 - 8x - 1)
t(x) = -5x3 + 4x2 + x - 7 - 7x4 - 2x3 + 8x + 1
t(x) = - 7x4 - 7x3 + 4x2 + 9x - 6
Determine the end behavior of the following function. Use proper notation.
k(x) = -3x(x + 5)2(x - 1)3(x + 10)
LT = -3x7
`As ` x ->-\infty, k(x) ->\infty
`As ` x ->\infty, k(x) ->-\infty
What would be the remainder when this function is divided by the factor (x - 2)?
The remainder would be 3 because f(2) = 3.
Determine the relative extrema.

Rel max: (-2, 2.9) & (3, 6)
Rel min: (-4, 0) & (0.5, -0.3)
Rewrite h(x) = (4x - 3)(7x2 - 2x4 + 3x - 8) in standard form.
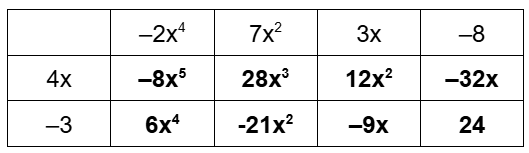
h(x) = -8x5 + 6x4 + 28x3 - 9x2 - 41x + 24
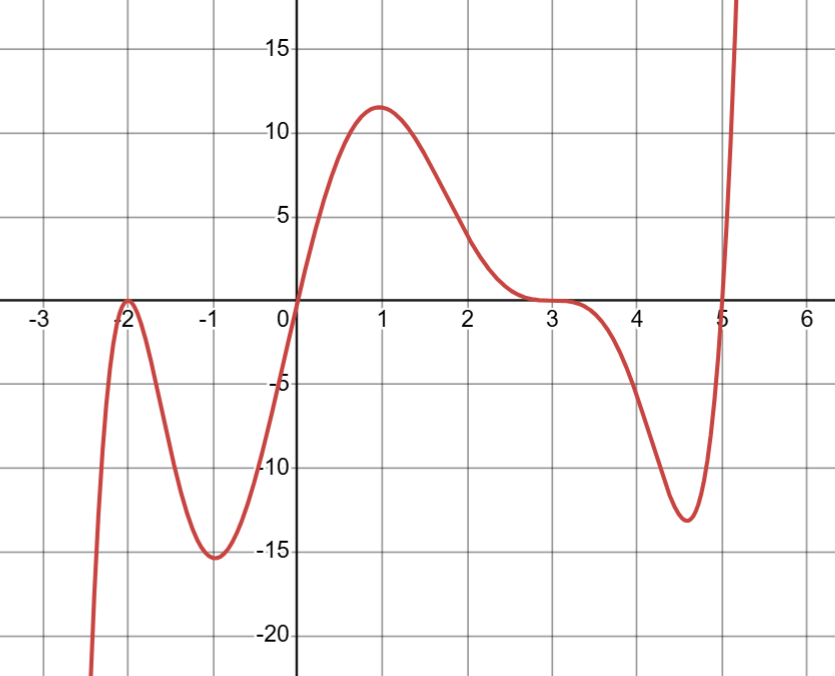
Write the equation of this function. You are given that the leading coefficient is 0.04.
y = 0.04x(x + 2)2(x - 3)3(x - 5)
We know that (x + 5) is a factor of
f(x)=x^3-5x^2+(3k+1)x+120
What is the value of k?
f(-5)=(-5)^3-5(-5)^2+(3k+1)(-5)+120
f(-5)=-125-125-15k-5+120
f(-5)=-135-15k
0 = -135-15k
135 = -15k
k=-9
Where is the function increasing and decreasing?
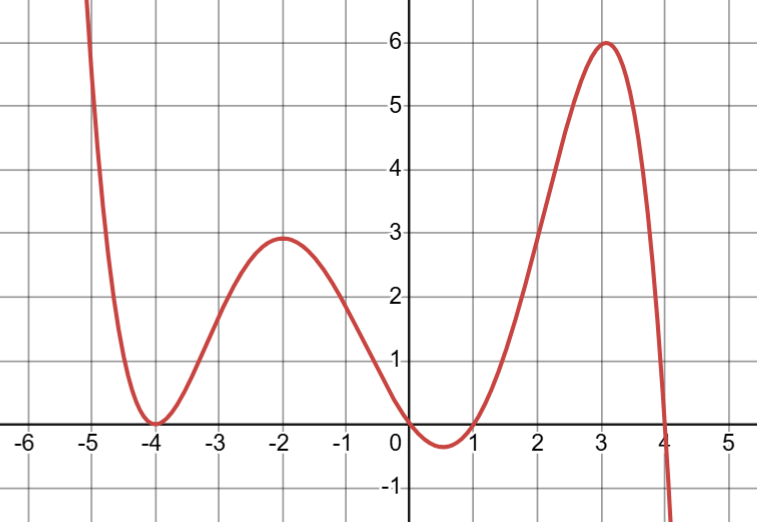
Inc: (-4, -2) U (0.5, 3)
`Dec: `(-\infty,-4)` U `(-2,0.5)` U `(3,\infty)
We are given that f(x) = 3x2 - x + 4, g(x) = 2x + 3, and h(x) = 8x3 + 5x - 7. Determine the standard form of the equation r(x) = 2h(x) - f(x)g(x)
r(x)=2(8x^3+5x-7)-(3x^2-x+4)(2x+3)
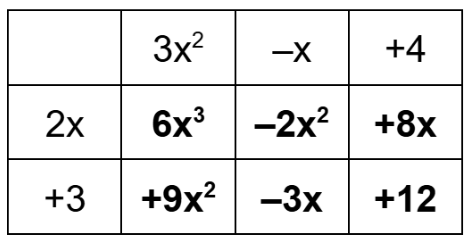
r(x)=(16x^3+10x-14)-(6x^3+7x^2+5x+12)
r(x) = 10x^3-7x^2+5x-26
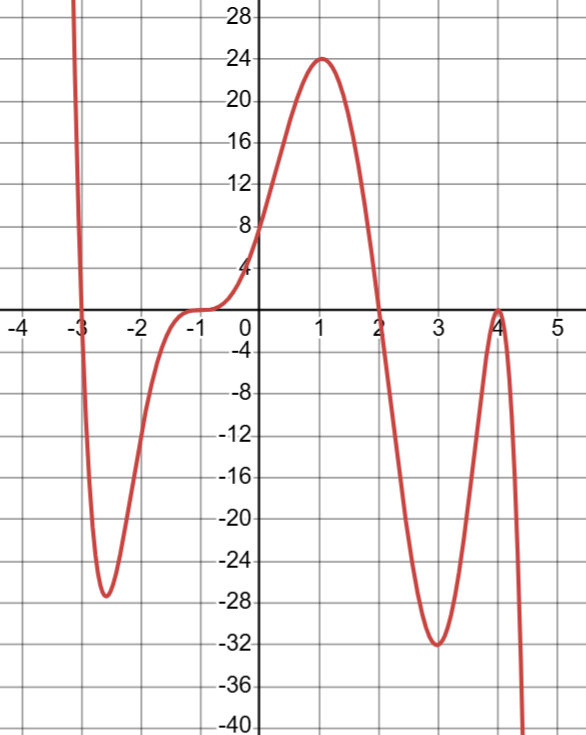
Sketch the graph of the following function. Include x and y intercepts.
f(x)=-frac{1}{12}(x-4)^2(x+1)^3(x-2)(x+3)
The function given below has a relative maximum at (4, 0). Find the equation of f(x) in factored form.
f(x)=x^4-19x^3+128x^2-368x+384
Rel. max at (4, 0) means that (x - 4) is a factor with a multiplicity of 2 (function degree is 4).
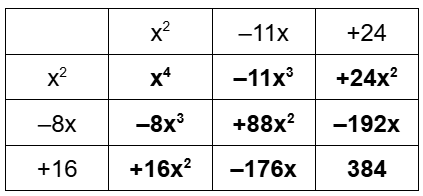
f(x)= (x - 4)2(x2 - 11x + 24)
f(x) = (x - 4)2(x - 8)(x - 3)
Where is the function positive and negative?

`Pos: `(-\infty,-4)` U `(-4, 0)` U `(1,4)
`Neg: `(0, 1)` U `(4,\infty)