Adding/Subtracting Polynomials
Multiplying Polynomials
Name That Polynomial
polynomial graphs
Division/Remainder
100
Add the Polynomials
(4x + 9) +(x - 4)
5x + 5
100
Multiply the Polynomials:
3x2 (2x4)
6x6
100
f(x) = -12x
What is a Linear Monomial?
100
What is the degree and leading coefficient?
f(x)=-5x^5+3x^3-3x+1
D:5
LC:-5
100
What would I put on the outside of the synthetic division box when dividing by (x - 4)
4
200
Subtract the polynomials:
(-5h - 2) - (7h +6)
-12h - 8
200
Find the result when 3x3+4x2-5x-2 is divided by x+2.
3x2 - 2x -1
200
f(x) = 4x2+3x+1
Quadratic Trinomial
200
What do we know about the leading term of this graph?
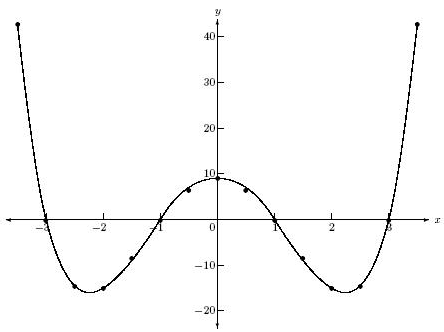
Degree: Even
L.C.: Positive
200
What would I put in the synthetic division box when I divide 3x^5 - 2x^3 +x^2 - 5x + 12
3 0 -2 1 -5 12
300
Add the polynomials:
(x2 +3x + 5) + ( -x2 +6x)
9x + 5
300
Multiply the Polynomials:
(2m - 1)(m + 2)
2m2 + 3m - 2
300
f(x) = 3- x2
Quadratic Binomial
300
Describe end behavior (using infinity)
As x 
As x
300
What is the solution to this division problem?
(x^2 - 10x +21) divided by (x - 3) ?
(x - 7)
400
Add the polynomials:
(t2 + 3t3 -3) + (2t2 +7t -2t3)
t3 +3t2 +7t -3
400
Multiply the Polynomials:
(d + 3)(d2 - 4d + 1)
d3 - d2 -11d + 3
400
f(x) = 3x3 +x2 -2x+ 2
Cubic polynomial
400
Describe End Behavior (using infinity)
As x
As x
400
What is the remainder of this division problem?
x^3 - 2x^2 + x - 5 divided by x - 2
- 3
500
Subtract the Polynomials:
(k2 + 6k3 -4) - (5k3 + 7k -3k2)
k3 + 4k2 -7k -4
500
Find the result when x4-10x2+11 is divided by x+1.
x^3-x^2-9x+9+2/(x+1)
500
f(x) = 1
Constant Monomial
500
Describe the following for the graph:
Leading coefficient, degree, zeros, y intercept
L.C.: positive
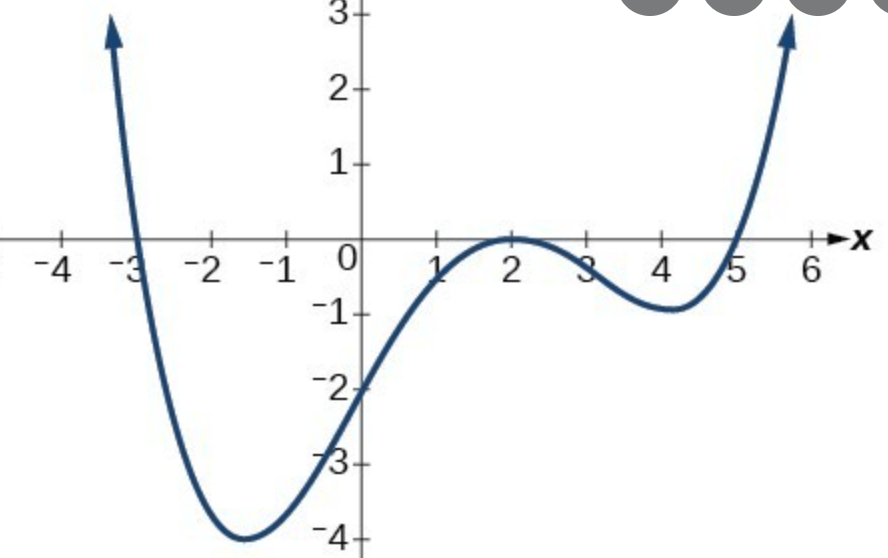
Degree: even
Zeros: -3, 2, 5
Y-int: -2
500
What would the quotient be when I divide
3x^4 - 5x^2 - 7x + 1 by (x - 2)
3x^3 + 6x^2 + 7x + 7 + 15/(x-2)