Ch 6
Ch 5
Ch 7
Ch 8
Ch 9
Unit Circle
100
1. Find the radian measure of -135 degrees.
2. Find the degree measure of
(4pi)/3
1.
-(3pi)/4
2. 240 degrees
100
The point P (x,y) is on the unit circle in Q4. Find y if
x=sqrt55 /8
-3/8
100
simplify:
1/sec(t)
cos(t)
100
Convert to rectangular coordinates:
(9,(5pi)/4)
(-9/sqrt2, -9/sqrt2)
100
Find the vector with initial point (5,-7) and terminal point (-2,1). Then find the magnitude of that vector.
-7i+8j
sqrt113
100
evaluate
sin ((5pi)/6)
1/2
200
Find:
tan(theta)+sin(theta)
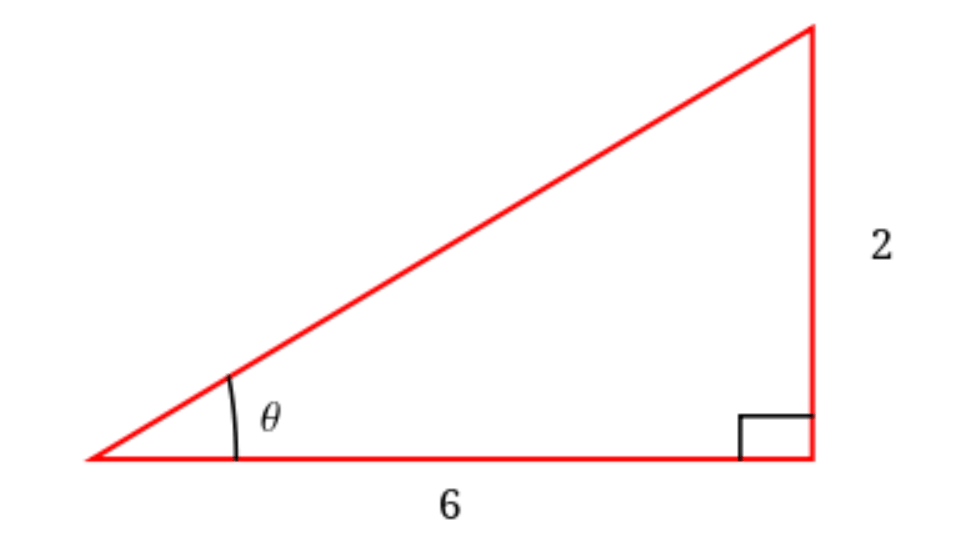
1/30(10+3sqrt10)
200
The point P is in Q2 and has y-coordinate 12/13. Find sin(t), cos(t), tan(t), sec(t).
sin(t) = 12/13
cos(t) = -5/13
tan(t) = -12/5
sec(t) = -13/5
200
simplify:
1-sin^2(t)
cos^2(t)
200
Convert to polar coordinates: one with positive r value and one with negative r value.
(-12,4sqrt3)
(8sqrt3,(5pi)/6)
(-8sqrt3,(11pi)/6)
200
Find the dot product. What does it tell us about the two vectors?
u= <4,3>, v= <-6,8>
0, the two vectors are orthogonal
200
evaluate
cos((15pi)/4)
sqrt2 /2
300
The base of a ladder is 6 ft from a building, and the angle formed by the ladder and the ground is 76 degrees. How high up the building does the ladder touch?
24.1 ft
300
What is the amplitude, period, and horizontal shift:
y=-2sin(2/3x-pi/6)
amplitude = 2
horizontal shift =
pi/4
period =
3pi
300
sin(pi/12)
(sqrt6-sqrt2)/4
300
Convert the equation to rectangular coordinates:
r=8cos(theta)
(x-4)^2+y^2=16
300
Find the length and direction of u:
u=<4sqrt3,-4>
length = 8
direction = 330 degrees or 11pi/6
300
evaluate
tan(-(4pi)/3)
-sqrt3
400
Find x.
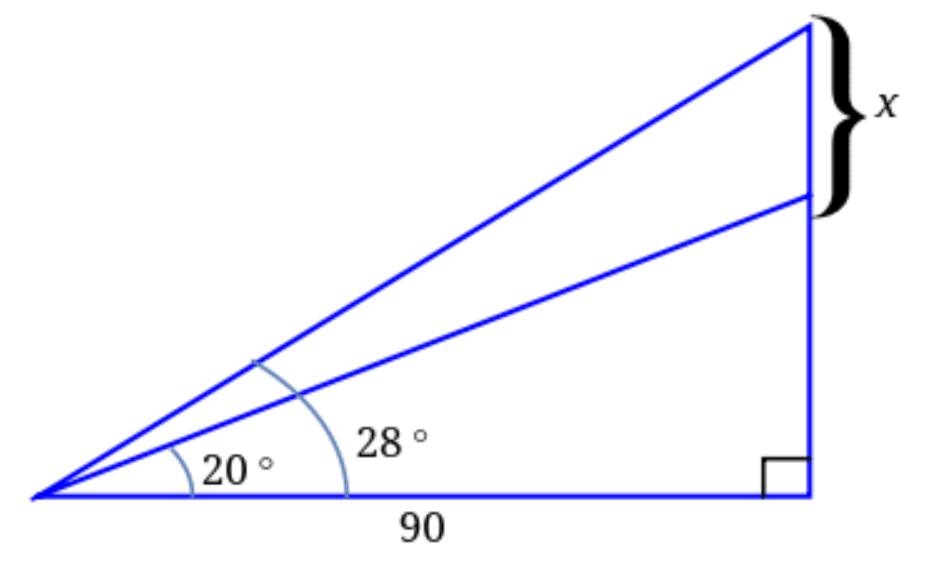
15.1
400
evaluate:
cos^(-1)(-sqrt2/2)
(3pi)/4
400
Solve the trig equation in the interval [0, 2pi):
2cos^2(theta)+19cos(theta)+9=0
theta=(2pi)/3,(4pi)/3
400
Write in polar form:
z=8+8sqrt3 i
16cis pi/3
400
Find u x v.
u= i+j-3k
v= 2i-5j+k
-14i-7j-7k
400
evaluate
csc((7pi)/2)
-1
500
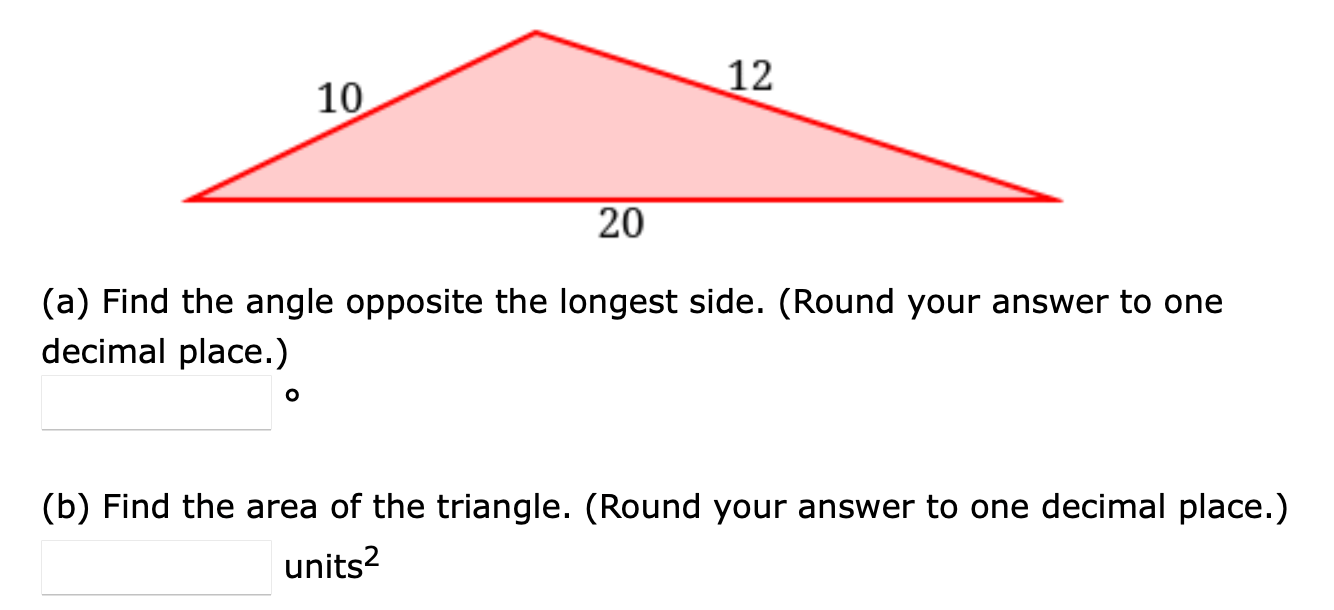
a) 130.5 degrees
b) 45.6 square units
500
If cos(t) = -8/17 and the terminal point is in Q3, find tan(t)*cot(t)+csc(t)
-2/15
500
solve the trig equation in the interval [0, 2pi):
2cos^2(x)+cos(2x)=0
x=pi/3,(2pi)/3,(4pi)/3,(5pi)/3
500
z1*z2 = -12
z1/z2 =
sqrt3/6+1/6i
500
Find a unit vector that is orthogonal to both j+5k and i-3j+2k.
<17/(3sqrt35),5/(3sqrt35),-1/(3sqrt35)>
500
evaluate
sec(-pi/2)
undefined