Algebra
Concepts
Angles in Standard
Radians
Arcs & Sectors
100
Expand (2x+3)^2
4x^2+12x+9
100
If a function f(x) is one to one, how will the domain and range of f(x) compare with the domain and range of f^-1(x) ?
The domain and range of a function and its inverse are interchanged.
100
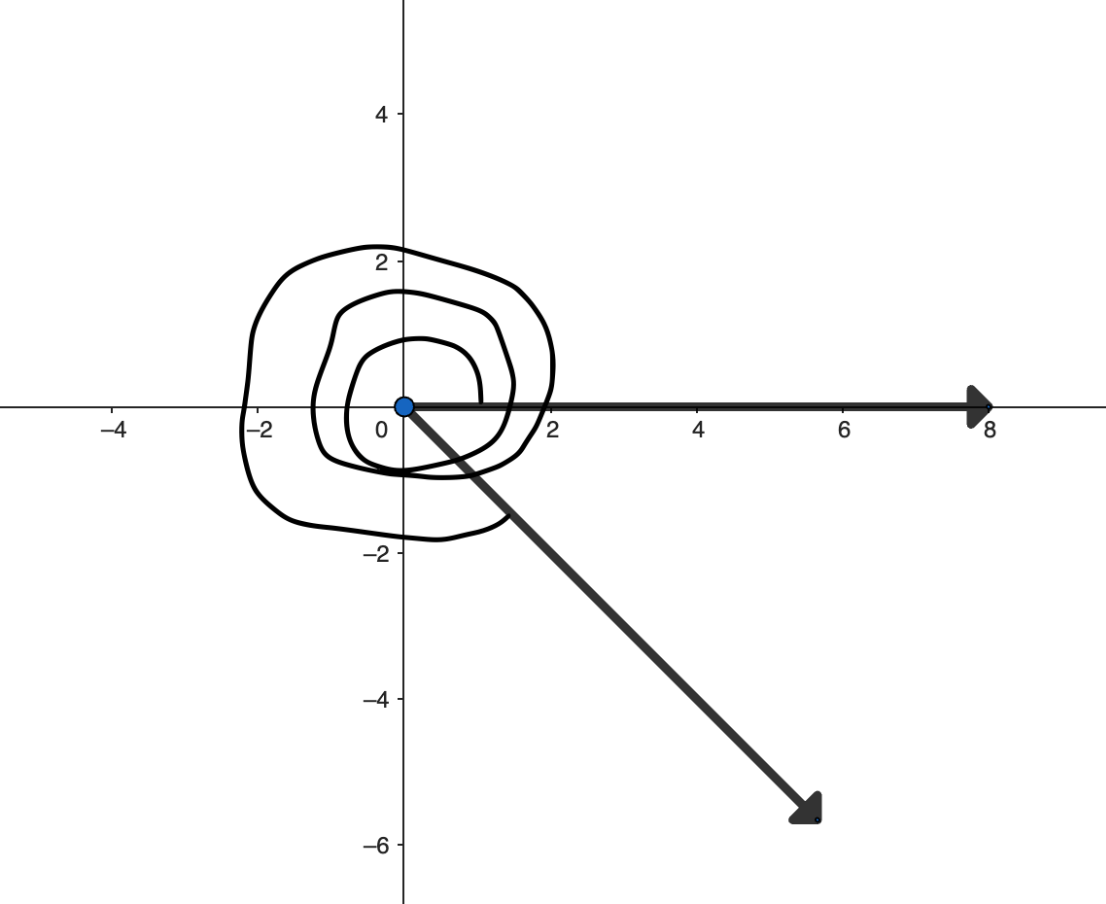
Graph the following angle in standard position:
\frac{23\pi}{4}
100
Convert each to degrees.
1. \frac{\pi}{4}
2. \frac{\pi}{3}
3. \frac{\pi}{6}
1. 45 degrees
2. 60 degrees
3. 30 degrees
100
A circular sector has a radius of 3cm and a central angle of \frac{2pi}{5} . Calculate the arc length of the sector.
\frac{6\pi}{5}cm
200
Given f(x)=x^2+3x+2 and g(x)=sqrt{x+1} evaluate
f(g(x))
x+3sqrt{x+1}+3
200
True or false: A sector angle in radians can be found using the following formula \frac{"arc length"}{"radius"}
True
200
State one positive, one negative, and the general form of all coterminal angles to
\frac{4\pi }{5}
\frac{4\pi }{5} + 2\pi k, k\in\mathbb{Z}
200
Convert to radians:
1. -135 degrees
2. 100 degrees
-\frac{3\pi}{4}
\frac{5\pi}{9}
200
Find the area of the sector of a circle if C=10\pi cm and \theta=\frac{7\pi}{4} .
\frac{175\pi}{8}
300
Fully simplify, noting domain restrictions as necessary.
\frac{\frac{2}{x}-1}{\frac{x-7}{10}+\frac{1}{x}}
\frac{-10}{x-5} , x!=0,2
300
Given functions f(x)=x^2 and
g(x)=e^x , determine if the following compositions would be even, odd, or neither:
1. f(g(x))
2. g(f(x))
1. Neither
2. Even
300
If one full rotation is 8 Miller units, state the general form for all coterminal angles to 3 Miller units.
3+8k, k\in\mathbb{Z}
300
Convert 4 radians to degrees.
\frac{720}{\pi} deg
300
A circular sector has an arc length of 6cm and an area of 9cm^2 . Determine the radius and central angle of the sector.
r=3cm
\theta=2rad
400
Given f(x)=x^3+10 , evaluate and simplify: \frac{f(x+h)-f(x)}{h}
3x^2+3xh+h^2
400
Given functions f(x)=2|x|+4 and g(x)=\root{3}{x} determine if the following would be even, odd, or neither:
1. f(x)+g(x)
2. f(g(x))
3. g(f(x))
1. Neither
2. Even
3. Even
400
Graph -2 radians in standard position.
400
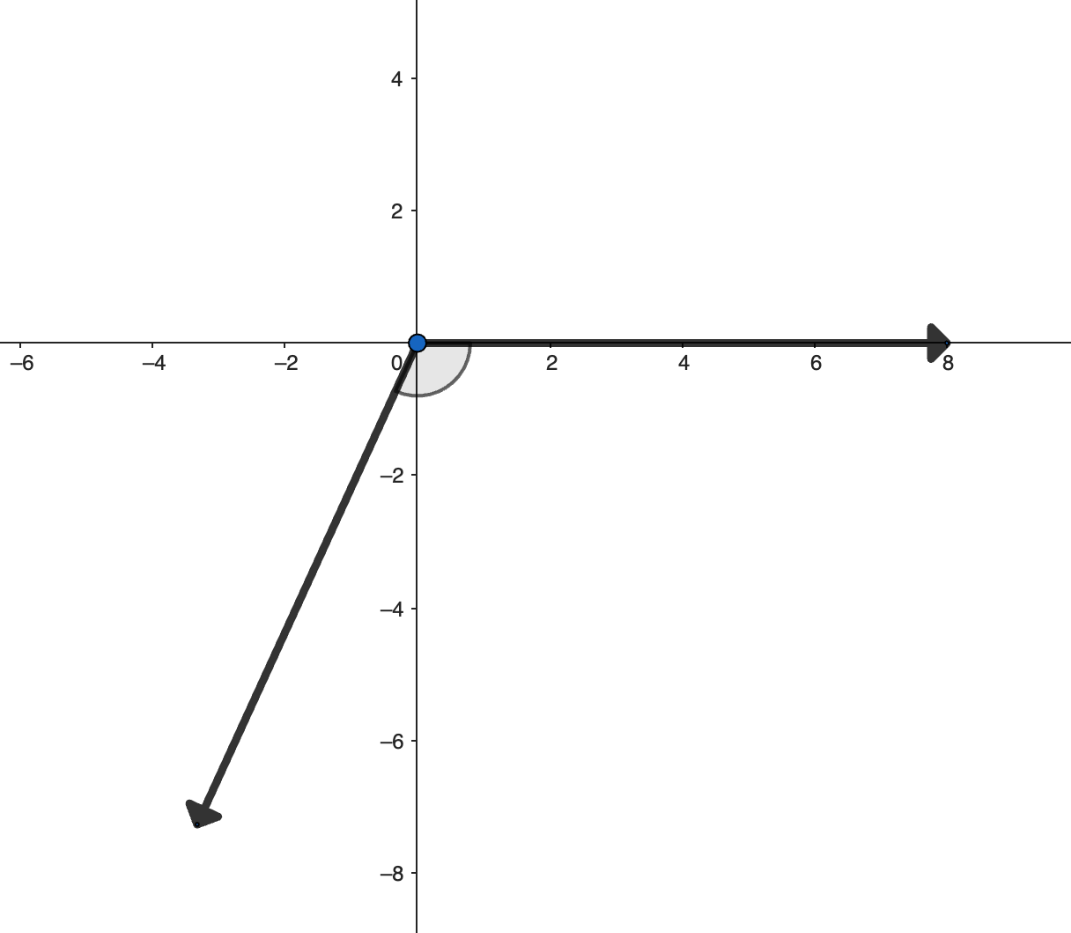
Which is bigger, 1/2rad or \frac{pi}{2}deg ?
1/2 a radian
400
Sectors C and D exist on the same circle, with central angles A and B respectively. If the arc length of Sector C is 4\pi "cm" and the area of Sector D is 4\pi "cm"^2 , determine the ratio of \frac{A^2}{B} .
\frac{2\pi}{1}