Functions
Analyzing Graphs and extrema
Continuity and end behavior
Transformations and inverse functions
Operations and Composition of functions
100
Does the table represent a function?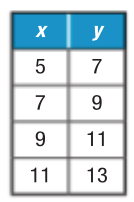
Yes
100
Find the domain and range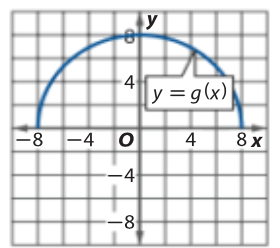
D= [-8,8] R=[0,8]
100
Is the function continuous at the the given value x=4?
f(x)=x^2-3x
yes continuous,
f(x)=4
100
Identify the parent function and the transformations
g(x)= sqrt(x-3)+2
f(x)=sqrtx
up two and right three
100
Find
(f*g)(x) and (f/g)(x)
f(x)=4x^2-1
g(x)=5x-1
(f*g)(x)=20x^3-4x^2-5x+1
(f/g)(x)=(4x^2-1)/(5x-1)
200
Find f(5) for
f(x)=x^2-3x+4
14
200
Find Domain and Range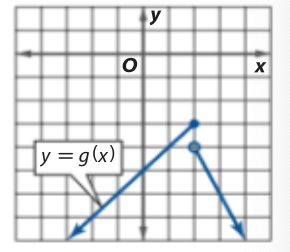
D=(-oo,oo) R=(-oo,-3)
200
Is the function continuous? if not, state the type of discontinuity and where it is discontinuous.
f(x)=x/(x+7)
infinite discontinuity at x=-7
200
Identify the parent function and the transformations
g(x)=-(x-6)^2-5
f(x)=x^2
down 5 right 6 reflection over x
200
find
(f@g)(x)
f(x)=1/(x-3)
g(x)=2x-6
(f@g)(x)=1/(2x-9
300
Find f(-3x) for
f(x)=x^2-3x+4
9x^2+9x+4
300
Find y int. and zeros of
f(x)=x^2-6x-27
y-int: -27
zeros: -3, 9
300
Is the function continuous? if not, state the type of discontinuity and where it is discontinuous.
f(x)=(x^2+2x-8)/(x-2)
Point discontinuity at x=2
300
Determine if a inverse function exists and if so what it would be for
f(x)=-(3)/(x+6)
Yes,
f^-1(x)=(-3)/x-6
300
Find
(f@g)(x)
f(x)=4x+11
g(x)=2x^-8
(f@g)(x)=8x^2-43
400
State the domain of
g(x)=sqrt(6x-3)
x>=1/2
400
Use the graph to estimate the increasing/decreasing intervals to the nearest .5 unit and classify extrema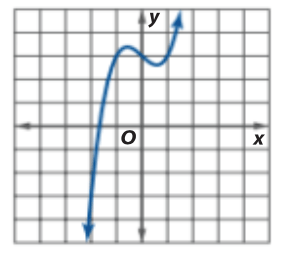 
increasing:
(-oo, -0.5) & (0.5, oo)
decreasing:
(-0.5, 0.5)
Rel max: (-0.5, 3.5) Rel min (0.5, 2.5)
400
Describe the end behavior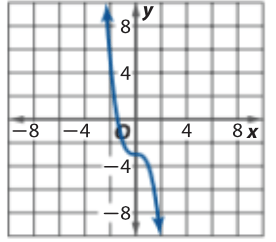 
lim_(x->oo)f(x)->-oo
lim_(x->-oo)f(x)->oo
400
Find the inverse function and state any restrictions on the domain
f(x)=x^3-2
f^-1(x)=root(3)(x+2)
400
Find
(f@g)(x), (g@f)(x), and (f@g)(2)
f(x)=x^2+2x+8
g(x)=x-5
(f@g)(x)=x^2-8x-23
(g@f)(x)=x^2+2x+3
(f@g)(2)=11
500
Find domain of
h(x)=x^2/(x(x^2-4)
x!=0, +-2
500
Find the average rate of change of the function on the interval [0,2]
f(x)=-x^3+3x+1
-1
500
describe the end behavior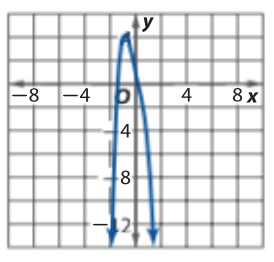
lim_(x->oo)f(x)->-oo
lim_(x->-oo)f(x)->-oo
500
Find the inverse function and state any restrictions on the domain
f(x)=x/(x+2)
f^-1(x)=(-2x)/(x-1)
x!=1
500
find two functions such that
h(x)=(f@g)(x)
h(x)=sqrt(x^3-4)
f(x)=sqrtx
g(x)=x^3-4