Angles and Radians
Triangles and Points
Graph Basics
Graph Transformations
Solving and Logic
100
convert 135o to radians. Give your answer in terms of pi
(3pi)/4
100
The point (-4/5, -3/5) lies on the unit circle. Find the value of secx
secx = 1/cosx = 1/(x value on unit circle) = -5/4 or -1.25
100
Period of sinx
2pi
100
range of y = 4sin(x - 90o)
-4<=y<=4
100
In which quadrants is cosecant (csc) positive?
Quadrant 1 and Quadrant 2 (same place sin is positive)
200
Angle of
(16pi)/3
Find a coterminal angle between 0 and
2pi
(4pi)/3
200
a. sin21 = a/13 --> 4.7
b. cos21 = b/13 --> 12.1
200
Range of secx
y <=-1 uu y >=1
200
give three asymptotes of y = cot(x/2)
... ,-4pi, -2pi, 0, 2pi, 4pi, 6pi, ...
200
Which quadrant has cosx < 0 and cotx > 0?
Quadrant 3
300
Find the reference angle for
(16pi)/3
pi/3
300
The angle of elevation to the top of a building from a point on the ground 30 yards from its base is 37°. Find the height of the building to the nearest yard.
tan37 = x/30 --> x = 22.607 = 23 yards
300
Asymptotes between -2pi and 2pi for tanx
-3pi/2, -pi/2, pi/2, 3pi/2
300
Range of y = 5tan(3x - pi/6) + 4
All real numbers
300
If cos u = 1/3 and tan u < 0, find the value of u in degrees. Round to two decimal places
cos-1(1/3) = 70.53o but tan < 0 so should be in quadrant 4.
reference angle 70.53o
actual angle u = 360 - 70.53 = 289.47o
400
Find the arc length: Circle with radius of 20 feet. Central angle of 75o. Round to two decimal places if needed.
1. convert 75o to radians
2. s =
r*theta = (5pi)/12 * 20
Answer: 26.18 feet
400
A 73-foot rope from the top of a circus tent pole is anchored to the flat ground 43 feet from the bottom of the pole. Find the angle, to the nearest tenth of a degree, that the rope makes with the pole.
in your drawing, looking for the top angle not the bottom angle.
sinx = 43/73 --> sin-1(43/73) = x --> x = 36.1o
400
What's the difference between tanx and cotx graphs?
tanx goes up, cotx goes down.
tanx goes through (0,0). cotx has an asymptote at x = 0
400
Write a sin equation for the graph below
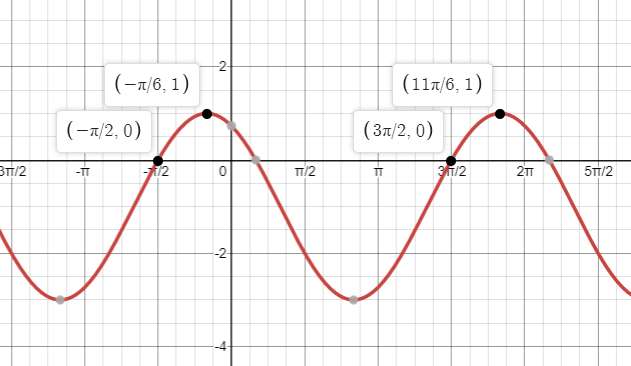
y = -2sin(x-pi/3)-1
400
If cotx = -3 and sinx > 0, then secx = ?. Round to two decimal places
cotx < 0 and sinx>0 means x is in quadrant 2 and secx < 0
cotx = -3 --> tanx = -1/3 --> tan-1(-1/3) =-18.43o
Reference angle = 18.43.
sec(18.43) 1/cos(18.43) = 1.05 but said in quadrant 2, secx is negative
final answer: - 1.05
500
A wind machine used to generate electricity has blades that are 10 feet in length. The propeller is rotating at four revolutions per second. Find the linear speed, in feet per second, of the tips of the blades.
1. convert from revolutions per second to radians per second (because revolutions isn't an exact distance)
4rev/sec * 2pi rad/rev = 8pi rad/sec
2. v = rw
v = 10 * 8pi = 80pi feet/sec
3. Round to 251.33 feet/sec
500
If (-2, 5) is a point on the terminal side of angle u, find the exact value of csc(u).
radius =
sqrt(29)
csc(u) =
1/sin(u)
=
sqrt(29)/5
500
What's the difference between secx and cscx graphs?
cscx has an asymptote at x = 0.
secx has a y-intercept at x = 0 (y = 1)
500
Write a sec equation for the graph below
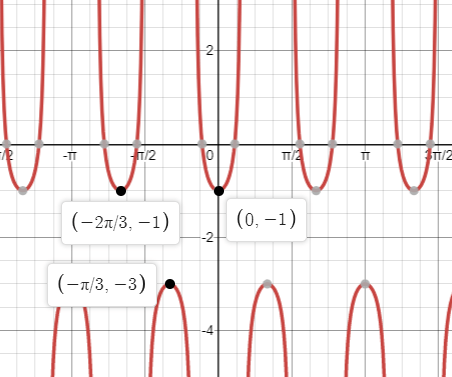
y = sec(3x) - 2
500
solve for x in radians: 4sec(x + pi/3) - 1 = 7
get to sec(x + pi/3) = 2
then 1/cos = sec
so 1/2 = cos(x + pi/3)
cos-1(1/2) = x + pi/3
x = cos-1(1/2) - pi/3 = 0