The domain of the quadratic function graphed here.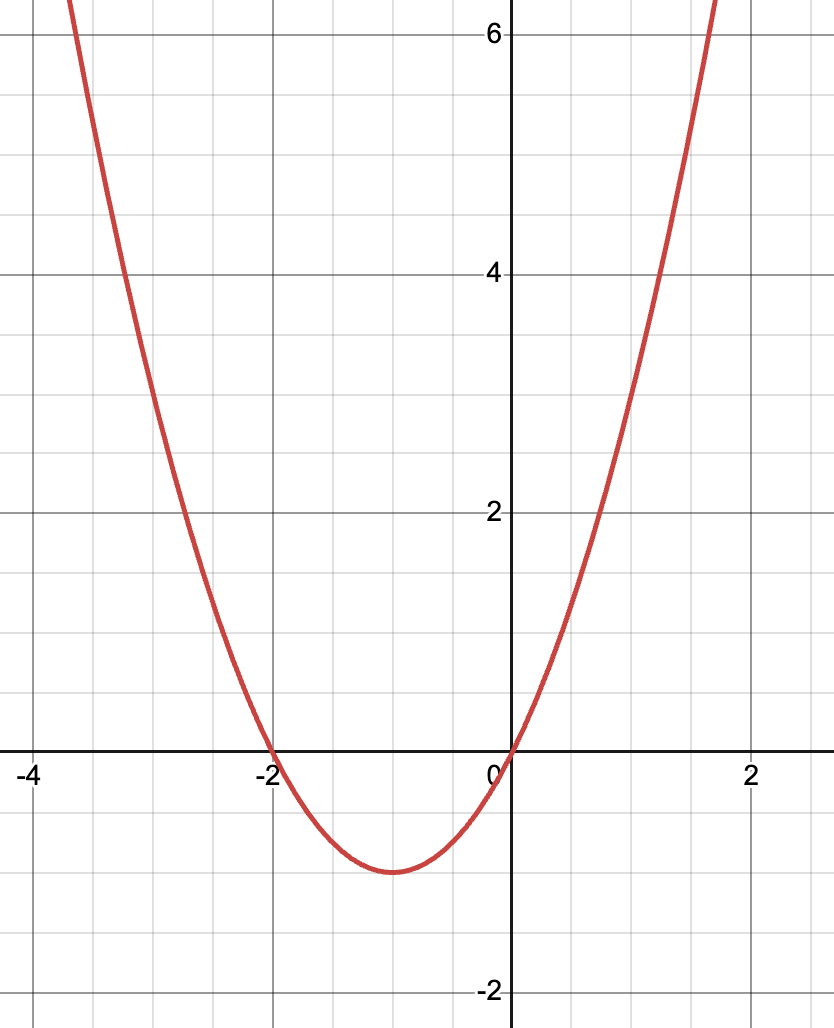
What is
(-oo,oo)
This type of asymptote usually affects the range of a function.
What is a horizontal asymptote?
Given an exponential function that models the change in temperature of a dish, the initial temperature of the dish is represented by this intercept.
What is the y-intercept?
...of a linear function
What is a linear function?
It's graph is shown here.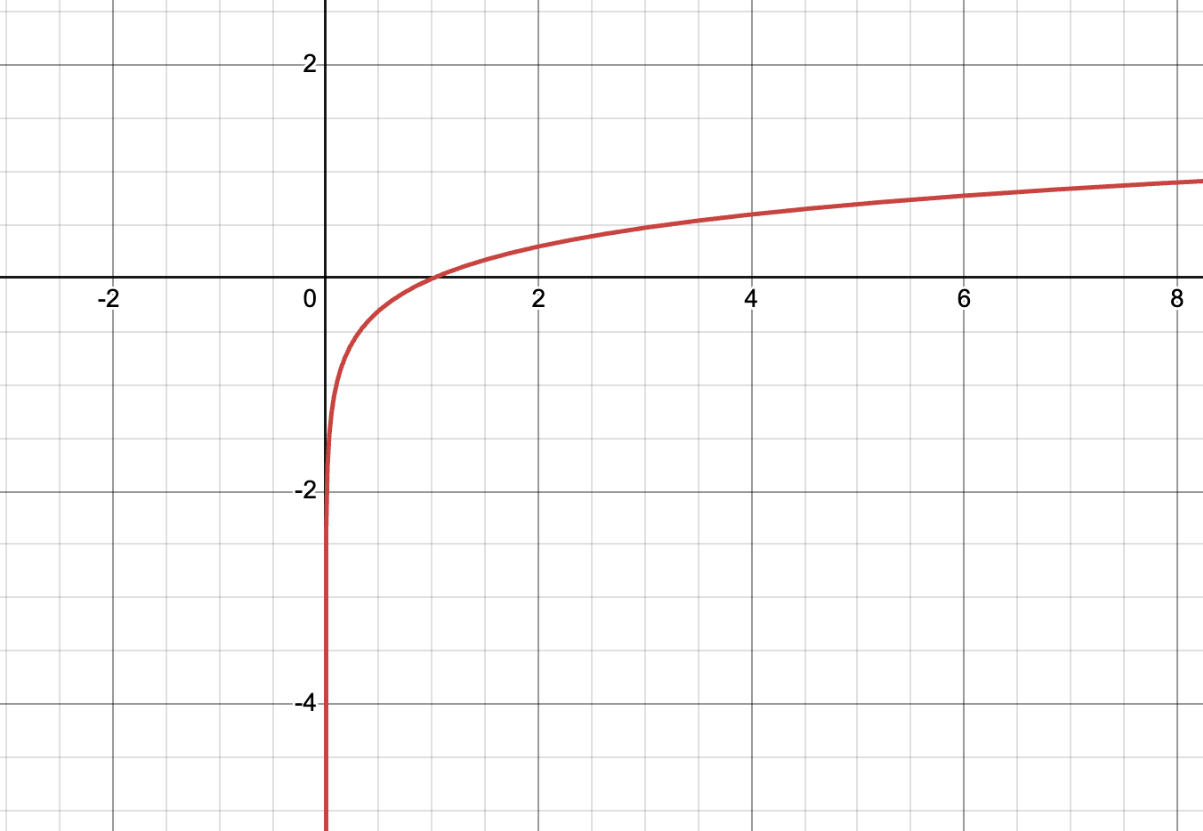
What is a log function?
The domain of this function is the range of a log function.
What is an exponential function?
The range of a quadratic function whose parabola is concave up with a vertex at (1,2).
What is
[2,oo)
The y intercept of
f(x)=x^2-2x+3
What is
(0,3)
...of y=log_2(x)
What is
y=2^x
It can be high maintenance, with horizontal asymptotes, vertical asymptotes, holes, oh my!
What is a rational function?
The domain of the log function
log_2(x+3)
What is
(-3,oo)
The range of the function
f(x)=sin(x-pi/3)+2
What is
[1,3]
The y intercept of g(x)=2cosx
What is
(0,2)
...of a tangent, sine, and cosine function, in that order.
what is a cotangent, a cosecant, and a secant function?
The period of this function can be found by calculating
pi/b
What is a tangent function?
The domain of a tangent function does not include these two values on the interval
0<=x<2pi
What are
x=pi/2 and (3pi)/2
The exponential function A=2000e^(.05t) represents the growth of a $2000 investment at a rate of 5% compounded continuously. This interval represents the range.
What is
[2000,oo)
The x intercepts of
f(x)=x^2-5x+6
What are
(3,0) and (2,0)
...of the relation {(1,2), (-2,3), (9,1)}
What is {(2,1), (3,-2), (1,9)}?
This function is used to calculate the value of an investment into an account that compounds interest annually
What is
A=P(1+r)^t
The domain of the rational function:
What is
(-oo,-3) (-3,2) (2,oo)
The range of the inverse of
f(x)=2*3^x-1
What is
(-oo,oo)
The x intercept of the rational function
f(x)=(x+5)/(x^2+1)
What is
(-5,0)
...of the function y=2x-1
What is
y=(1/2)x+(1/2)
This classification is reserved for relations that are functions, AND whose inverse is also a function.
What is a one-to-one function?