Laws of Logarithms
Inverse Trig
Quadrants
Graphing
Newton's Law of Cooling (Calculator Allowed)
Solving
(Calculator Allowed)
(Calculator Allowed)
100
Use laws of logarithms to expand.
log_5(3x^2)
log_5(3)+2log_5(x)
100
Evaluate
cos(cos^-1(-1/2))
-1/2
100
Find
cos(-pi/2)
0
100
Which of the following have a period of 2pi?
y=sinx
y=cosx
y=tanx
y=cscx
y=secx
y=cotx
y=sinx
y=cosx
y=cscx
y=secx
100
The temperature of a bowl of soup, in degrees Fahrenheit, is
68+60e^(-kt)
where is the time since it was served, measured in minutes.
Determine the temperature of the soup when it was served.
128 degrees
100
Solve for x.
e^(2x)+e^x-12=0
x=ln(3)
200
Use laws of logarithms to expand.
log((2x)/y)
log(2)+log(x)-log(y)
200
Evaluate
cos^-1(-sqrt3/2)
(5pi)/6
200
What quadrant is the angle in.
theta=(-7pi)/6
Quadrant 2
200
Write an equation with the starting point at
(pi/4,3)
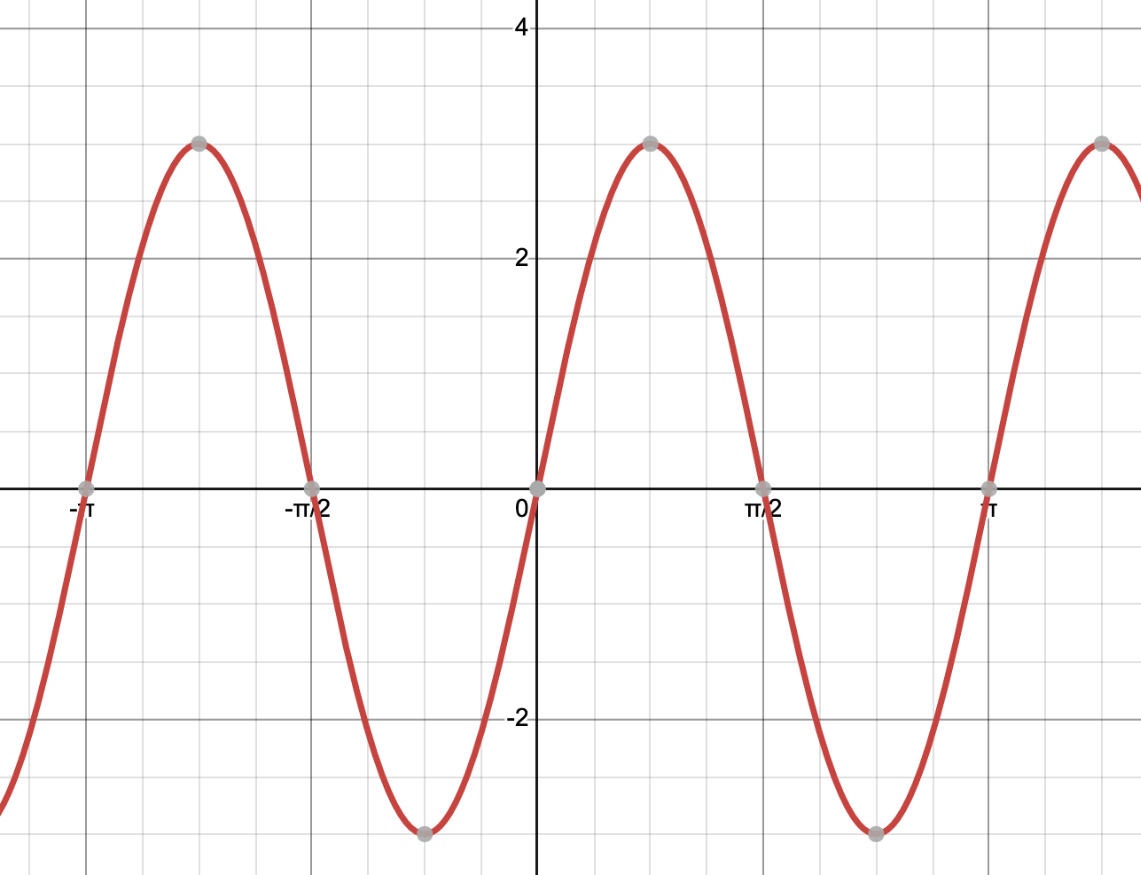
y=3cos(2(x-pi/4))
200
The temperature of a bowl of soup, in degrees Fahrenheit, is
72+58e^(-kt)
where is the time since it was served, measured in minutes.
Determine the temperature of the soup when it was served.
130 degrees
200
Solve for x.
e^(2x)+3*e^x-10=0
x=ln(2)
300
log2=x, log3=y and log7=z
Find log(14) in terms of x, y and z.
x+z
300
Evaluate
sin^-1(cos(pi/4))
pi/4
300
If
cos(theta)=-1/sqrt5 and sin(theta)=-2/sqrt5
Find
cot (theta)
1/2
300
Write an equation with the starting point
(pi/2,-2)
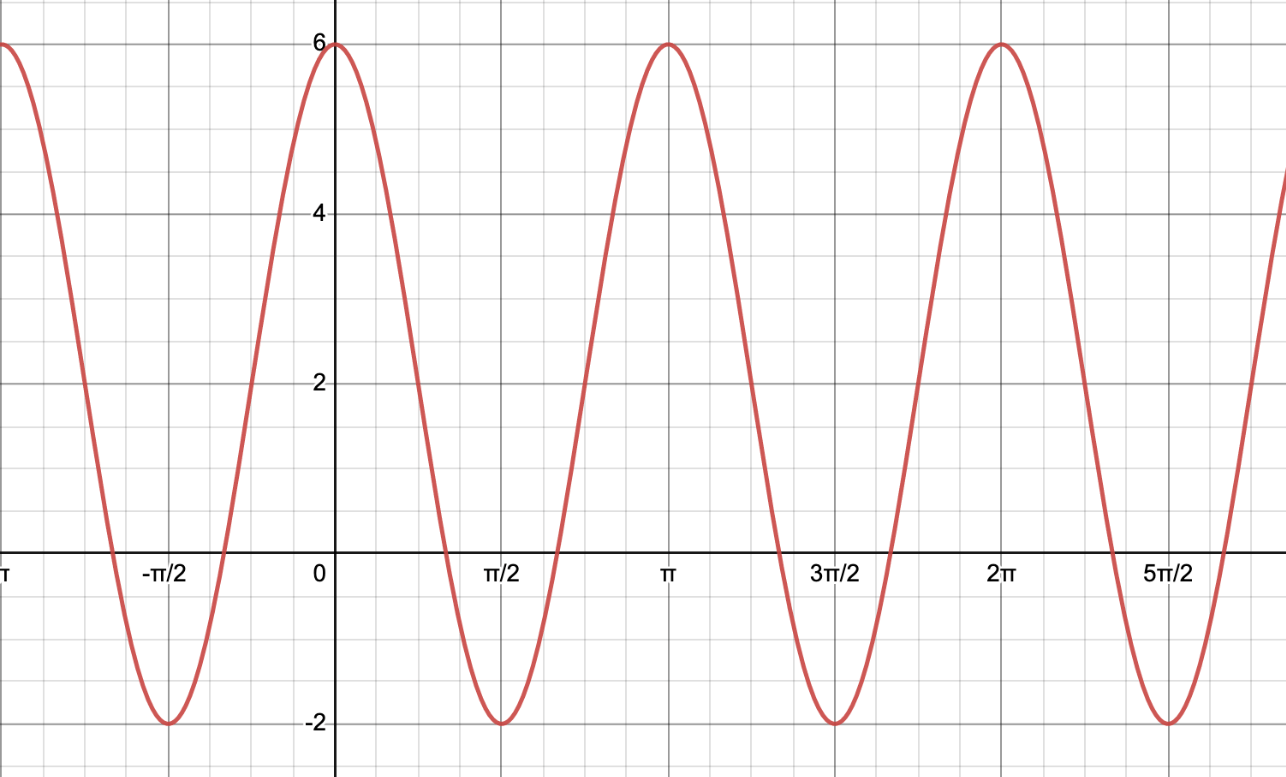
y=-4cos(2(x-pi/2))+2
300
The temperature of a bowl of soup, in degrees Fahrenheit, is
68+60e^(-kt)
where is the time since it was served, measured in minutes.
If the soup is 100 degrees after 8 minutes, find the value of k.
k=0.079
300
Solve for x.
3^(2x)+5*3^x-6=0
x=0
400
log2=x, log3=y and log7=z
Find log(7/6) in terms of x, y and z.
z-(x+y)
400
Evaluate
sin(2cos^-1(sqrt3/2))
sqrt3/2
400
If
cos(theta)=9/10
and theta is in Quadrant 4, Find
csc (theta)
csc (theta)=10/-sqrt(19)
400
Write an equation with the starting point at
(pi/4,0)
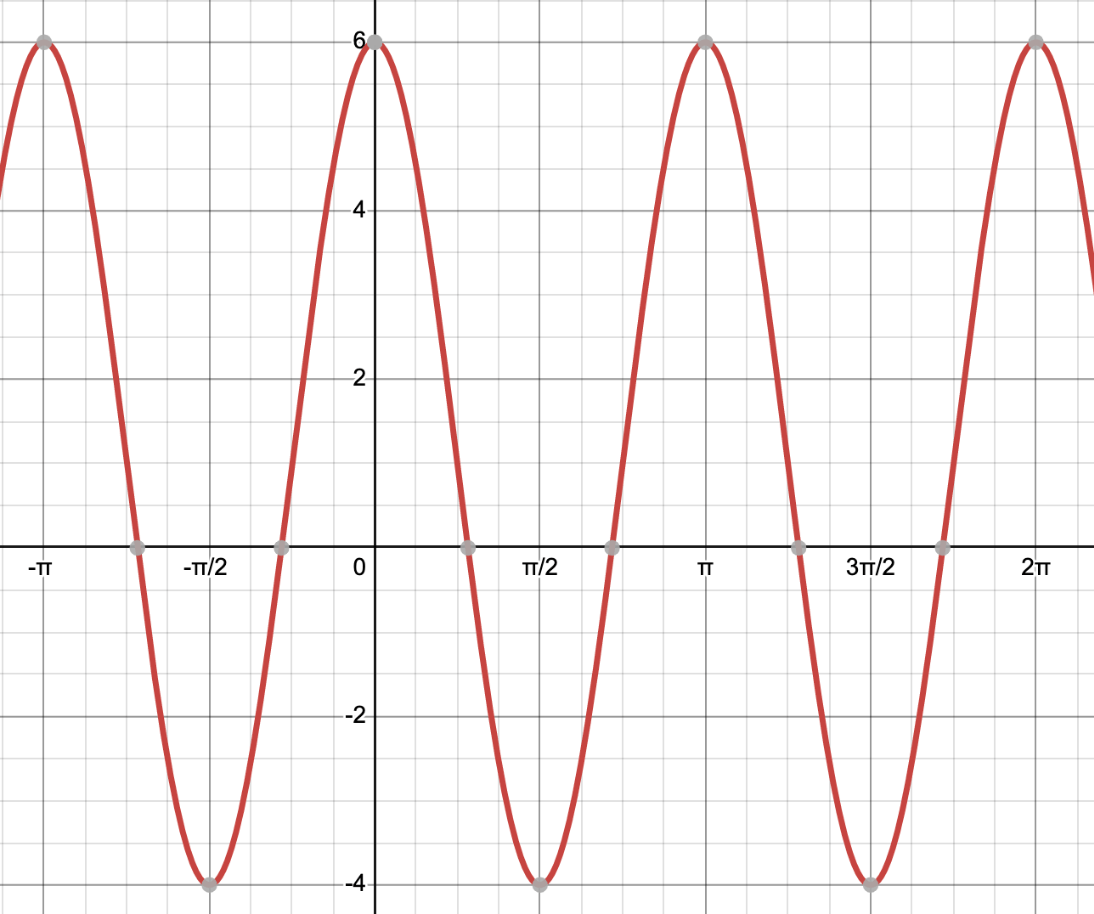
y=-5sin(2(x-pi/4))+1
400
The temperature of a bowl of soup, in degrees Fahrenheit, is
72+58e^(-kt)
where is the time since it was served, measured in minutes.
If the soup is 90 degrees after 7 minutes, find the value of k.
k= 0.167
400
Solve for x.
2^(2x)-5=-4*2^x
x=0