5.1/5.2
5.3
5.5
7.1
7.2/7.3
100
Convert to radian
315°
(7pi/4)
100
Is this the parent function of sine or cosine?
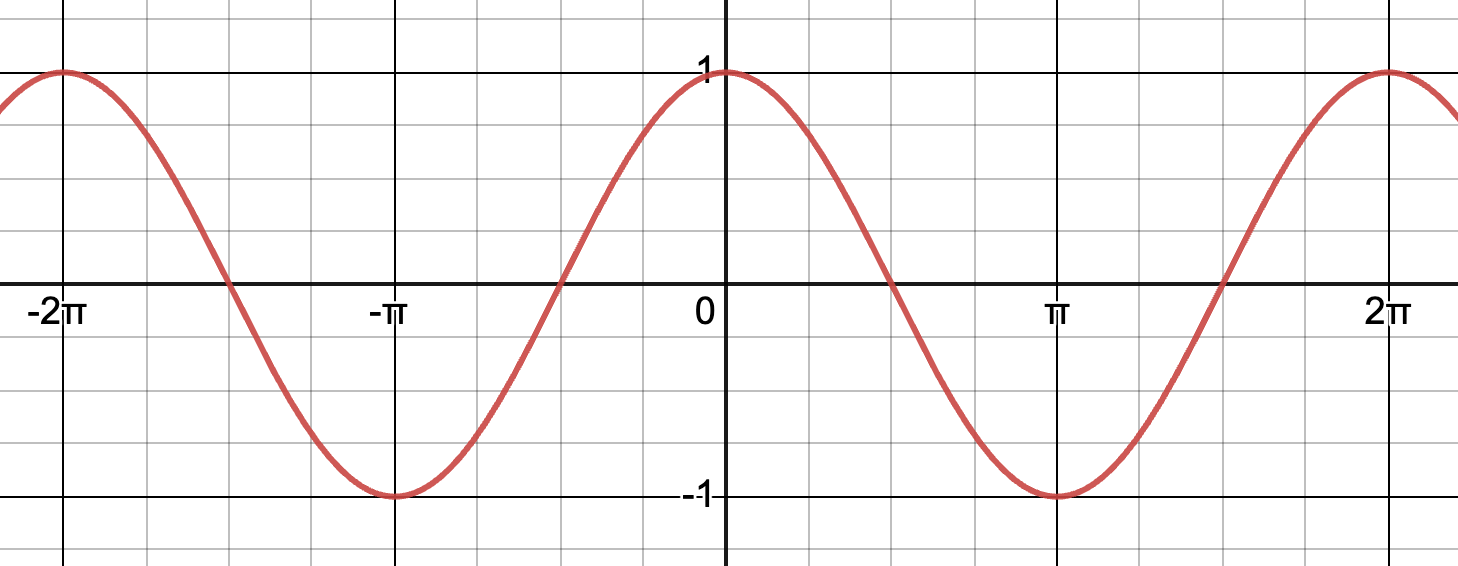
y=cos(x)
100
Domain and Range of inverse sine function
Domain [-1, 1]
Range [-π /2, π /2]
100
True or False: To prove an identity, we perform the same operations on both sides of the equation
False
100
Without calculator, calculate:
sin18°cos27° +cos18°sin27°
= sin(18°+27°) = sin(45°) = √2/2
200
What's the reference number of
(7pi)/4
pi/4
200
Identify the amplitude of the sine function
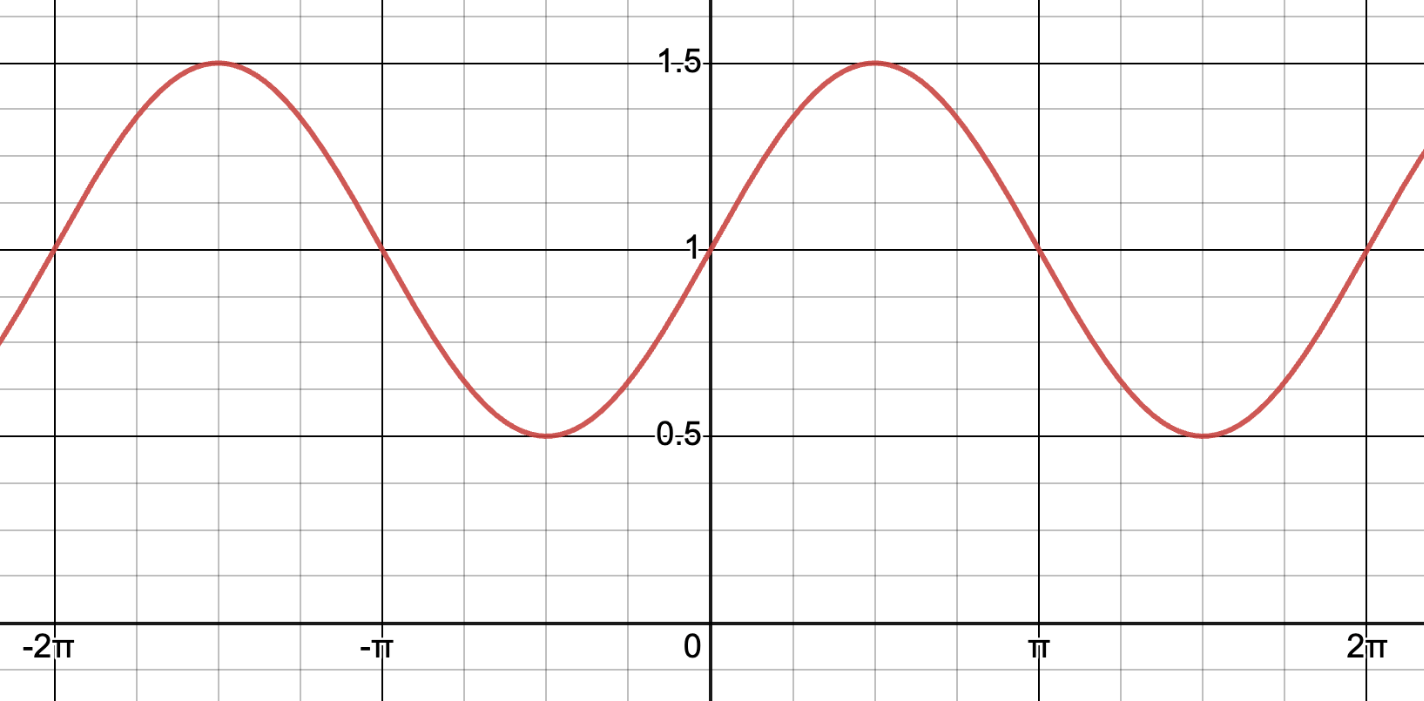
a = 0.5
200
To define the tangent function, we restrict the domain of tangent to the interval ____
[-π /2, π/2]
200
Simplify
cos(t)tan(t)
cos(t)*sin(t)/cos(t)=sin(t)
200
Simplify
sin8°/(1+cos8°)
=tan((8°)/2)=tan(4°)
300
P is a point on the unit circle in quadrant IV. Fill in the blank with the missing coordinate
P(__,-7/25)
P(24/25,-7/25)
300
Identify the horizontal shift of:
f(x)=7sin(πx-π /6)
1/6 right
300
cos^-1(cosx))=x
0 <= x <= π
300
Verify tan2x-cot2x=sec2x-csc2x
=sec2x-1-cot2x = sec2x-(1+cot2x) = sec2x-csc2x
300
Evaluate without a calculator
(tan(9pi/12)-tan(5pi/12))/(1+tan9pi/12*tan5pi/12)
tan(9pi/12-5pi/12)=tan(4pi/12)=tan(pi/3)=sqrt3
400
The terminal point determined by t is the point (-3/5, -4/5). What's the terminal point of
7π-t
(3/5, -4/5)
400
Identify the amplitude, frequency, and vertical shift of the cosine function.
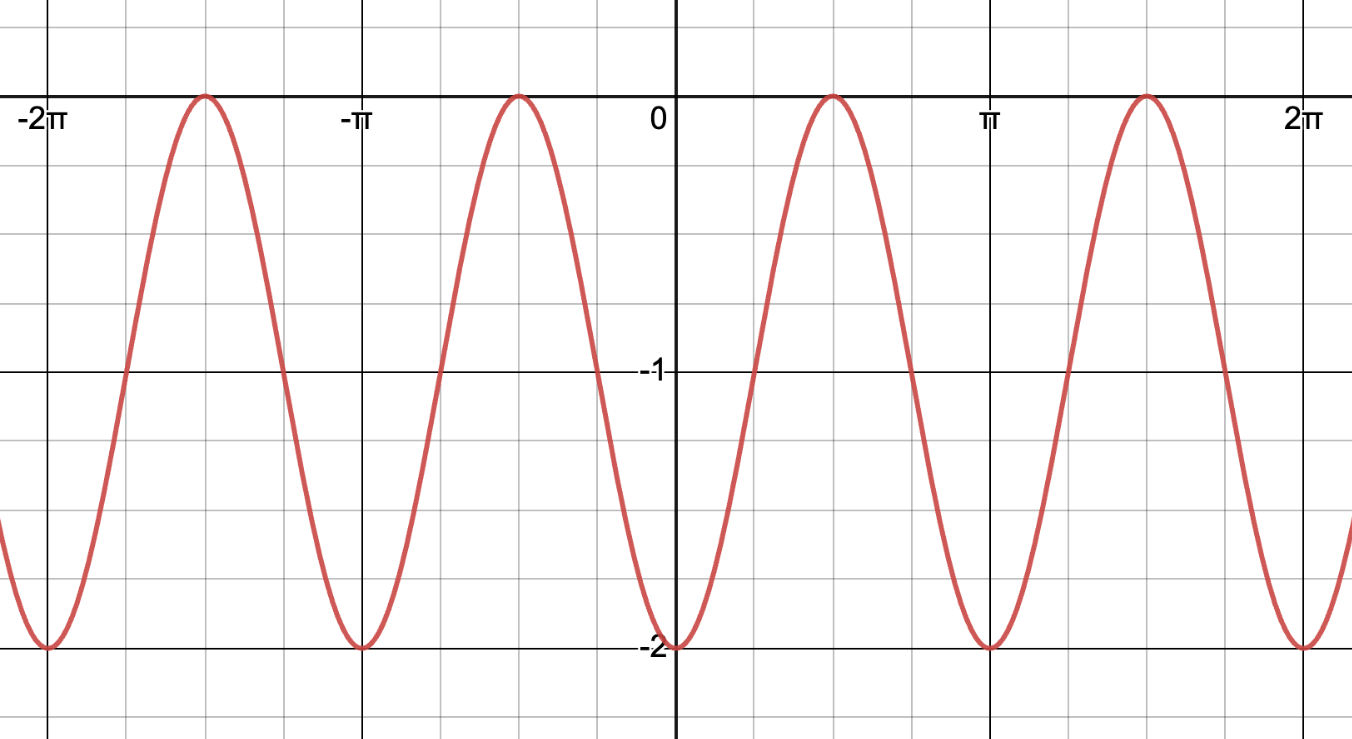
a=-1
B=2
k=-1
400
tan(tan^-1x)=x for ?
x ∈ R
400
Simplify
sin(theta)/(1+cos(theta))+(1+cos(theta))/sin(theta)
=(sin^2theta+(1+costheta)^2)/((sintheta(i+costheta))
=(1+1+2costheta)/sintheta(i+costheta)=2/sintheta
=2csctheta
400
Verify
cos4x-sin4x=cos2x
=(cos2x-sin2x)(cos2x+sin2x) =cos2x(1)
500
Find the value using the unit circle
tan ((7pi)/4)=
tan ((7pi)/4)=-1
500
Write an equation for the following function using sine:
y = 2sin(4x-pi/3)
500
Simplify the following expression
sin^-1(sin(7pi/6))
-pi/6
500
Simplify the trigonometric expression
cosx/(secx+tanx)
cosx/(1/cosx+sin/cosx) = cosx/((1+sinx)/cosx)
= cos^2x/(1+sinx) = (1-sin^2x)/1+sinx
=((1-sinx)(1+sinx))/(1+sinx)
=1-sinx
500
Verify
2/(tanx+cotx)=sin2x
^.^