Vocab 1
Vocab 2
Vocab 3
Vocab 4
Quadratic Functions & Polynomial Functions of a higher Degree
Real Zeros of Polynomial Functions & Complex Numbers
The Fundamental Theorem of Algebra & Rational Functions and Asymptotes & Graphs of Rational Functions
100
polynomial function
f(x)=a_n x^n+a_(n-1) x^(n-1)+⋯+a_2 x^2+a_1 x+a_0
100
constant function
f(x)=a
100
linear function
f(x)=mx+b
100
standard form of quadratic
f(x)=ax^2+bx+c
100
Describe how the graph
y=-(x-4)^2+1
is related to
y=x^2
.
RAX
L4
D1
100
Divide using long division.
(24x^2-x-8)/(3x-2)
8x+5+2/(3x-2)
100
Find all the zeros of the function, write the polynomial as a product of linear factors, use your factorization to determine the x-intercepts of the graph of the function.
f(x)=x^3-5x^2-7x+51
x=-3,4+-i
(x+3)(x-4-i)(x-4+i)
(-3,0)
200
vertex form of quadratic
f(x)=a(x-h)^2+k
200
minimum
lowest relative extrema
200
maximum
highest relative extrema
200
power function
f(x)=x^n
200
Describe the graph of the function and identify the vertex and any x-intercepts.
f(x)=(x-4)^2-4
R4, D4
Vertex: (4,-4)
x-int: (2,0), (6,0)
200
Use synthetic division.
(2x^3+6x^2-14x+9)/(x-1)
2x^2+8x-6+3/(x-1)
200
Find a polynomial function with real coefficients that has the given zeros: 2, -2, 2i
f(x)=x^4-16
300
extrema
relative maxima or minima
300
zeros
solutions to polynomial functions equal to zero
300
multiplicity
if a polynomial function yields a repeated zero
300
Intermediate Value Theorem
If (a,f(a)) and (b,f(b)) where f(a)nef(b) , then for any number d between f(a) and f(b) there must be a number c between a and b such that f(c)=d
300
Write the vertex form of the quadratic function that has the vertex (2,3) and passes through the point (0,2).
f(x)=-1/4(x-2)^2+3
300
Solve using the remainder theorem at f(-2).
f(x)=x^4+10x^3-24x^2+20x+44
-156
300
Find the domain of the function and any asymptotes.
(2-x)/(x+3)
Domain: All real numbers x except x=-3
V.A. x=-3
H.A. y=-1
400
division algorithm
f(x)=d(x)q(x)+r(x)
400
Remainder Theorem
If f(x)/(x-k) , then r=f(k)
400
rational zero test
possible rational zeros =
factors of constant term / factors of leading coefficient
400
imaginary unit
i=√(-1)
400
Describe the transformation of the function from f(x)=x3.
f(x)=-(x-1)^3+3
RAX
R1
U3
400
Verify that the factor (x-4) is a factor of
f(x)=x^3+4x^2-25x-28
. Find the remaining factors. List all the real zeros.
(x+1)(x+7)
x=4, -1, 7
400
Find the domain of the function and any asymptotes.
2/(x^2-3x-18)
Domain: All real numbers x except x = 6, -3
V.A. x=-3, x=6
H.A. y=0
500
complex number
a+bi
500
pure imaginary number
bi
500
Fundamental Theorem of Algebra
If f(x) is a polynomial of degree n , where , then f has at least one zero in the complex number system.
500
Linear Factorization Theorem
If f(x) is a polynomial of degree n , where n>0 , then f has precisely n linear factors f(x)=a_n (x-c_1 )(x-c_2 )⋯(x-c_n ) where c_1,c_2,⋯,c_n are complex numbers.
500
Use the Leading Coefficient Test to describe the end behaviors of the graph.
-x^5-7x^2+10x
Up, Down
500
Use the Rational Zero Test and list all the possible rational zeros.
f(x)=10x^3+21x^2-x-6
+-1,+-2,+-3,+-6,+-1/10,+-1/5,+-3/10,+-2/5,+-1/2,+-3/5,+-6/5,+-3/2
500
Find the domain of the function and any asymptotes.
(7+x)/(7-x)
Domain: All real numbers x except x=7
V.A. x=7
H.A. y=-1
600
conjugates
Let f(x) be a polynomial function that has real coefficients. If a+bi , where b≠0 , is a zero of the function, then a-bi is also a zero of the function.
600
rational function
f(x)=(N(x))/(D(x) )
600
vertical asymptote
The line x=a of the graph of f when f(x)→∞ or f(x)→-∞ as x→a , either from the right or from the left
600
horizontal asymptote
The line y=b of the graph f when f(x)→b as x→∞ or x→-∞.
600
Find the zeros algebraically and approximate any zeros using a graphing utility.
f(x)=x(x+3)^2
x=-3, -3, 0
600
Use Descartes’s Rule of Signs to determine the possible number of positive and negative real zeros.
3 or 1 positive real zero
0 negative real zeros
600
Find all asymptotes and holes of the graph:
f(x)=(2x^2-7x+3)/(2x^2-3x-9)
V.A.: x=-3/2
H.A.: y=1
Hole: (3, 5/9)
700
1st step of graphing rational functions
Simplify f , if possible.
700
2nd step of graphing rational functions
Find and plot the -intercept.
700
3rd step of graphing rational functions
Find the zeros of the numerator.
700
4th step of graphing rational functions
Find the zeros of the denominator.
700
Find a polynomial function that has the given zeros.
-2, 1, 1, 5
f(x)=x^4-5x^3-3x^2+17x-10
700
Solve and write the result in standard form.
sqrt(-9)+3+sqrt(-36)
3+9i
700
Sketch the function
f(x)=(2x-1)/(x-5)
800
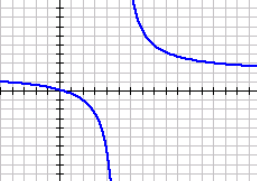
5th step of graphing rational functions
Find and sketch any other asymptotes.
800
6th step of graphing rational functions
Plot at least one point between and one point beyond each x-intercept and vertical asymptote.
800
7th step of graphing rational functions
Use smooth curves to complete the graph.
800
oblique asymptote
If the degree of the numerator is exactly one more than the degree of denominator, the graph of the function has this kind of asymptote.
800
Use the Intermediate Value Theorem and a graphing utility to find graphically any intervals length 1 in which the polynomial function is guaranteed to have a zero. Use the zero or root feature of the graphing utility to approximate the real zeros of the function.
f(x)=2x^4+7/2x^3-2
(-2,-1), (0,1)
x=-1.897, 0.738
800
Write the quotient in standard form.
(1-7i)/(2+3i)
-19/13-17/13i
800
C. S=-3.49t^2+76.3t+5958
R^2~~0.8915
E. Cubic; The cubic model more closely follows the pattern of the data.
F. 7157 stations