Simplify and express in standard form:
i17 + i11 +i6
-1
Find the coordinates of the y-intercept of:
f(x)= 2x2 + 8x + 11
(0 ,11)
Given f(x)= 2(x+3)2(x+1)(x-2)3, find the zeros and their multiplicities.
x=-3, mult. 2 ; x=-1, mult. 1 ; x=2, mult. 3
Given f(x) = (x2 - 1) / (x2 + 5x + 6) :
find the coordinates of all intercepts.
(-1, 0) , (1, 0) , (0, -1/6)
For the function below, write the domain and range using interval notation:
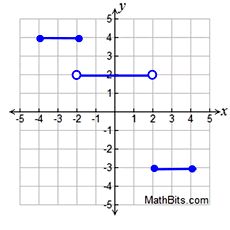
x ∈ [-4, 4]
y ∈ [-3] U [2] U [4]
Simplify and express in standard form:
(7 - i) - (2 - 3i)
5 + 2i
Find the coordinates of the vertex of:
f(x)= (x - 2)2 + 4
(2, 4)
Given f(x)= 2(x+3)2(x+1)(x-2)3, find the end behavior.
f(x) = 2x6
Given f(x) = (x2 - 1) / (x2 + 5x + 6) :
find the equations of all asymptotes.
x = -2, x = -3, y = 1
For the function below, write the domain and range using interval notation:
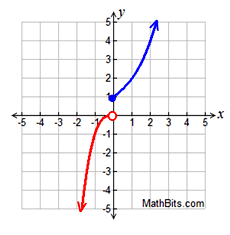
x ∈ [-∞ , ∞]
y ∈ (-∞ , 0) U [1, ∞)
Simplify and express in standard form:
(5 - 6i)2
-11 - 60i
Find the coordinates of the vertex of:
f(x)= 2x2 + 8x + 11
(-2, 3)
Given f(x)= 2(x+3)2(x+1)(x-2)3, find the coordinates of the y-intercept.
(0, -144)
Find the equation of the oblique asymptote of
f(x) = (5x2 + 2x - 7) / (x + 3)
y = 5x - 13
Graph the following piecewise function:

*
Simplify and express in standard form:
8 / (8 + 9i)
64/145 - (72/145)i
Write an equation for a quadratic function g(x) with a vertex of (-1, 3) and passes through the point (-3, -5)
g(x) = -2(x + 1)2 + 3
Write the equation for the graph of g(x):
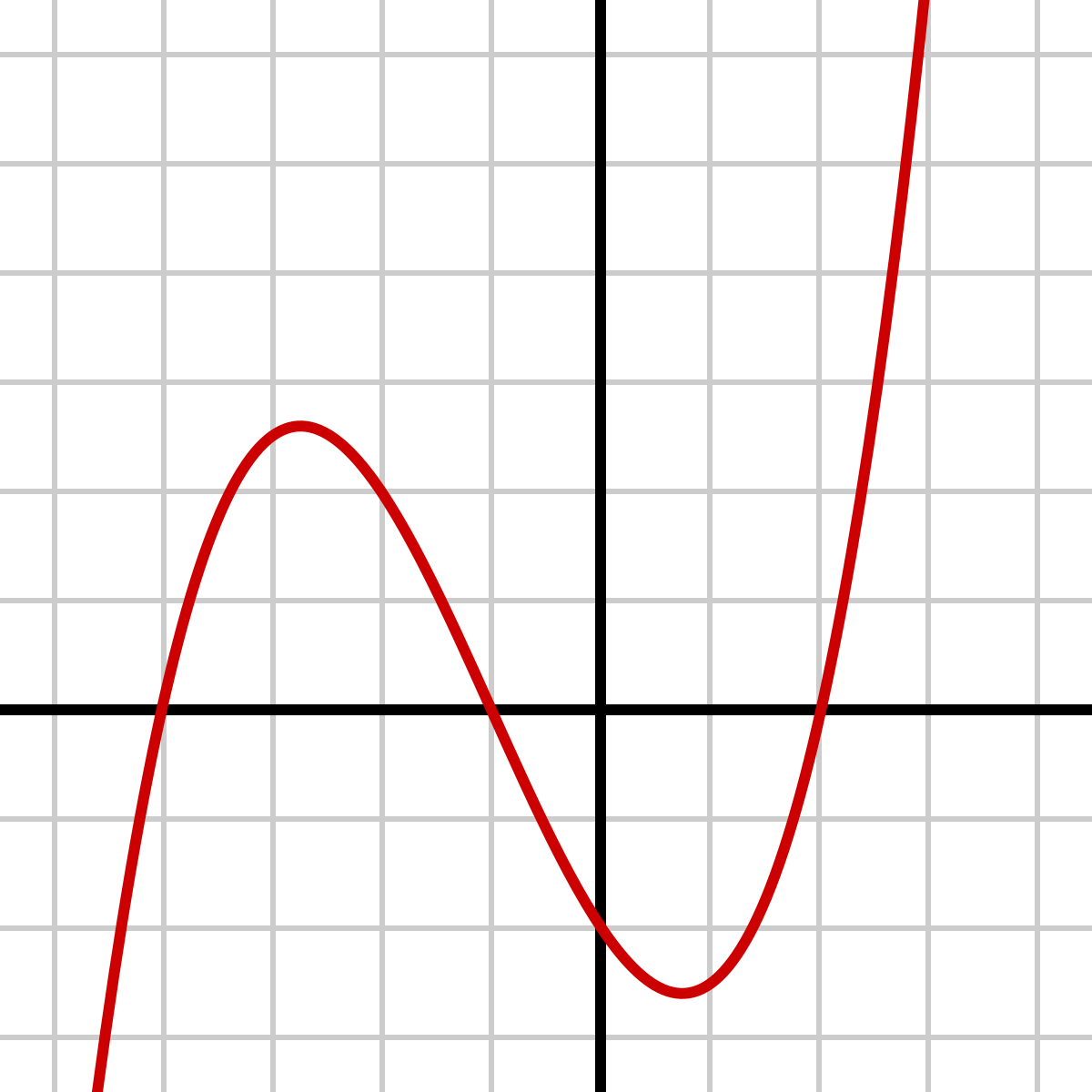
g(x) = 0.25(x+4)(x+1)(x-2)
Given f(x) = (x2 + x - 6) / (x2 - 5x + 6) :
find the coordinates of the hole.
(2, -5)
Graph the following piecewise function:
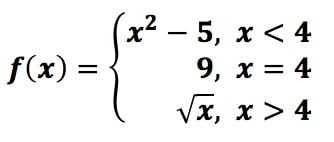
*
Simplify and express in standard form:
( -6 + 5i ) / ( -5 + i )
35/26 - (19/26)i
An apple is thrown into the air. Its height (in feet above the ground) as a function of time (in seconds) is given by h(t) = -4.9t2 + 12t + 5. What is the maximum height the apple reaches? Round your answer to the nearest thousandth.
h(t) = 12.347 feet
A rectangle has a length of 10 units and a width of 4 units. Squares of x by x units are cut out of each corner, and then sides are folded up to create an open box. Express the volume of the box as a polynomial function V(x) in terms of x. Leave your answer in factored form.
V(x) = x(10 - 2x)(4 - 2x)
Given the graph of f(x) below, write the equation of the function:

f(x) = [ 2(x - 2)(x - 5) ] / [ (x + 1)(x - 5) ]
For the function below, write the domain and range using set builder notation:

{x| x ∈ ℝ , x < 2, x ≠ 1}
{y| y ∈ ℝ, y ≤ 2, y ≠ 0}