SET
Applicable Axioms
Shrinking Universes
On My Own
Confusing Card Combinations
100
Two sets A and B that do not overlap,
A \cap B = \phi
What is mutually exclusive?
100
Something which is never negative!
What is probability?
100
The formula for conditional probability \mathbb{P}[A | B]
What is (assuming \mathbb{P}[B] > 0 )
\mathbb{P}[A | B] = \frac{\mathbb{P}[A \cap B]}{\mathbb{P}[B]} ?
100
The property that lets us multiply the probability of events:
\mathbb{P}[A_1 \cap \cdots \cap A_n] = \mathbb{P}[A_1]\ \cdots\ \mathbb{P}[A_n]
What is independence?
100
The number of ways to make k selections out of n items (without replacement, order independent).
What is n choose k?
200
(A cup B)^c = A^c cap B^c
(A cap B)^c = A^c cup B^c
What are De Morgan's Rules?
200
\mathbb{P}[ \Omega]= 1
What is the normalization property?
200
The probability that A occurs and B does not occur.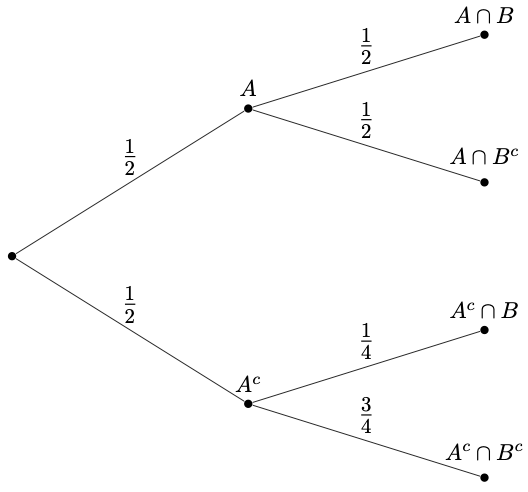
What is 1/4?
200
The probability
\mathbb{P}[A | B \cap C]
if we know that the events A, B, and C are independent.
What is
\mathbb{P}[A] ?
200
Consider a bag with 3 blue balls and 2 red balls. The probability that we grab two balls (simultaneously) and they are different colors.
What is 3/5?
300
\text{Sets }A_1,\ldots,A_n
such that
A_1 \cup \cdots \cup A_n = \Omega
What are collectivity exhaustive sets?
300
Property that is required in order to add up the individual probabilities of events:
\mathbb{P}[A_1 \cup \cdots \cup A_n] = \mathbb{P}[A_1] + \cdots + \mathbb{P}[A_n]
What is mutually exclusivity? (Or mutually exclusive)
300
The probability that B occurs.
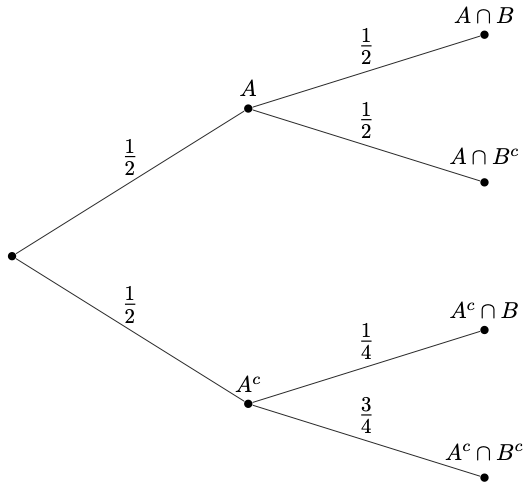
What is 3/8?
300
The property of events A, B, C satisfying
\mathbb{P}[A \cap B] = \mathbb{P}[A] \mathbb{P}[B]
\mathbb{P}[A \cap C] = \mathbb{P}[A] \mathbb{P}[C]
\mathbb{P}[B \cap C] = \mathbb{P}[B] \mathbb{P}[C]
What is pairwise independence?
300
Consider a bag with 3 blue balls and 2 red balls. The probability that we grab two balls (simultaneously) and they are the same color.
What is 2/5?
400
Sets A1, ... , An that are both collectively exhaustive and mutually exclusive.
What is a partition?
400
Formula for computing
\mathbb{P}[A \cup B]
assuming that A and B overlap.
What is
\mathbb{P}[A \cup B] = \mathbb{P}[A] + \mathbb{P}[B] - \mathbb{P}[A \cap B]
(inclusion-exclusion property)?
400
The probability of
\mathbb{P}[B|A]
in terms of
\mathbb{P}[A|B]
if we are also told that A is twice as likely as B,
\mathbb{P}[A] = 2\mathbb{P}[B]
What is
\frac{\mathbb{P}[A|B]}{2} ?
400
The property of events B, C, D satisfying
\mathbb{P}[B \cap C|D] = \mathbb{P}[B | D] \ \mathbb{P}[C|D]
What is conditional independence of B and C given D?
400
Consider a bag with 3 blue balls and 2 red balls. We grab two balls (simultaneously). Given that they are the same color, what is the probability they are blue?
What is 3/4?