Total Possible Outcomes (Sample Space)
Simple Probability
Compound Independent/Dependent
Experimental/
Theoretical
Theoretical
Likelihood
100
To find the number of outcomes in the sample space without making a list, tree, or table, use the __________ __________ __________.
What is the Fundamental Counting Principle?
100
If you roll a six-sided die, what is the probability of getting a 4? Write as a simplified fraction.
1/6
100
A coin is flipped and a die is rolled. What is the probability (simplified fraction) that the coin will land on heads and the die will land on a number greater than 5?
1/12
100
A coin is flipped 9 times and the results are below.
What is the experimental probability (simplified fraction) that the next coin that is flipped with land on tails?
4/9
100
There is a 25% change that it will rain tomorrow. Describe the likelihood that it will rain tomorrow.
What is unlikely?
200
How many total possible combinations (outcomes) are there when flipping a coin and rolling a die?
12
(2 x 6)
200
Amanda has 1 blue top, 5 pink tops, and 4 green tops in her closet. She randomly chooses one top out of her closet. What is the probability (simplified fraction) she chooses a green top?
2/5
200
Marge has cereal boxes in her pantry: 2 Cheerios, 3 Lucky Charms, 2 Fruit Loops, 2 Chex, and 1 Apple Jacks.
Marge will randomly choose one box of cereal. Then she will put it back and randomly choose another box of cereal. What is the probability (simplified fraction) that she will choose a box of Cheerios and then a box of Fruit Loops?
1/25
200
A spinner with equal sized sections is labeled A-C.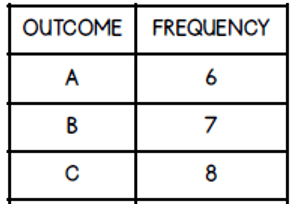 
What is the experimental probability (simplified fraction) that the next spin will be the letter B?
1/3
200
There are 2 red marbles and 6 blue marbles in a bag. What is the likelihood that you randomly choose a green marble out of the bag?
What is impossible?
300
How many total possible combinations (outcomes) are there when spinning a spinner with 4 equal sections and flipping a coin?
8
(4 x 2)
300
On James' shelf are 7 comedy DVDs, 6 drama DVDs, 5 horror DVDs, and 2 documentary DVDs.
James will randomly choose 1 DVD to watch. What is the probability (simplified fraction) that he will choose a documentary?
1/10
300
A spinner with 4 sections 1-4 is spun twice. What is the probability (simplified fraction) of spinning a 3 both times?
1/16
300
A number cube is rolled 20 times. Each time the number cube was rolled, the number showing on the top face was recorded. The table below shows the results.
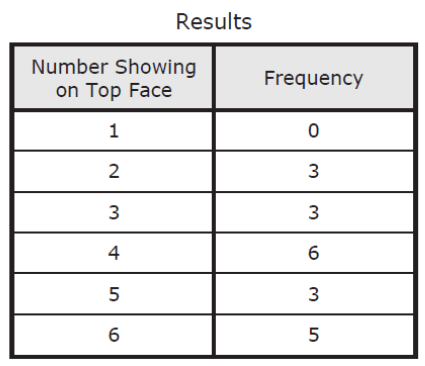
Based on these results, what is the experimental probability (simplified fraction) that the next time the number cube is rolled it will land with a 5 or 6 showing on the top face?
2/5
300
You flip a coin. What is the likelihood that you flip the coin and it lands on tails?
What is equally likely to happen or not happen?
400
At a restaurant you can choose from 3 different entrees, 4 different sides, and 2 different drinks. How many total possible combinations (outcomes) are there?
24
(3 x 4 x 2)
400
A bag contains colored tiles: 4 red tiles, 3 green tiles, and 5 blue tiles.
A tile will be randomly selected from the bag. What is the probability (in decimal form) that the tile selected will be green?
0.25
400
Beau has a bag of coins. The bag contains 10 dimes, 5 nickels, and 1 penny. He randomly selects a coin and puts it aside. He then selects a second coin.
What is the probability (simplified fraction) that Beau will select a dime first and then a penny?
1/24
400
A spinner with 4 equal sections labeled A-D is spun and the results are shown in the table below.
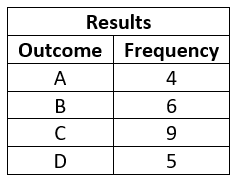
Which letter has the same theoretical probability as it does experimental probability?
B
400
A bag contains 20 purple marbles. What is the likelihood that you randomly choose a purple marble out of the bag?
What is certain?
500
How many outcomes are there when choosing a card from a standard deck of cards?
52
500
Rachael is setting up tables for a party. Four of the tables are covered with red tablecloths, and eight of the tables are covered with white tablecloths. Guests will be randomly seated at the tables when they arrive. Each table can seat 8 guests.
What is the probability (simplified fraction) that the first guest to arrive will be seated at a table with a red tablecloth?
1/3
500
A classroom is arranged with 2 seats in the front row, 4 seats in the middle row, and 6 seats in the back row. The teacher randomly assigns seats to students as they enter the classroom.
What is the probability (simplified fraction) that the first student who enters the classroom will be assigned a seat in the front row, and the second student who enters will be assigned a seat in the middle?
2/33
500
A coin is flipped and the results are shown below. What is the difference (as a simplified fraction) between the experimental and theoretical probabilities of flipping tails? (Hint: The difference between 10 and 8 is 2.)
1/8
500
How do you know if an event is likely to happen?
The probability of the event is greater than 50% and less than 100%.