Review of Probability
Venn Diagrams and Two Way Tables
Mutually Exclusive and Non Mutually Exclusive Events
Conditional Probability
Two Step Experiments
Tree Diagrams
Dependent and Independent Events
100
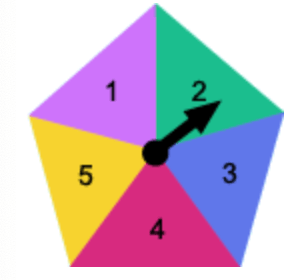
The chance of this spinner landing on 2 is:
20%
100
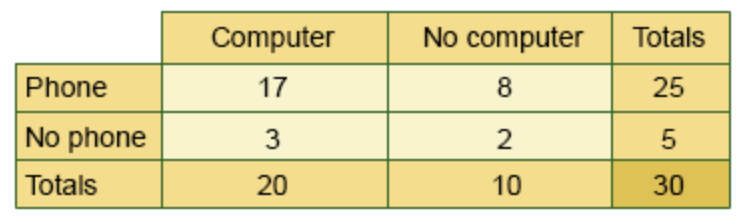
What is the probability of randomly choosing a student who does not own a phone?
1/6
100
In year 9 at Dartsure College, students can choose to study history or geography or both.
What is the probabilty (in simplest fraction form) that a randomly selected student studies history?
19/40
100
What is P(A|B)?
9/24
100
What is the probability of getting a tail when tossing a coin?
50%
100
Annie took two marbles from a bag containing three yellow marbles and two striped marbles, replacing the first marble before selecting the second one.
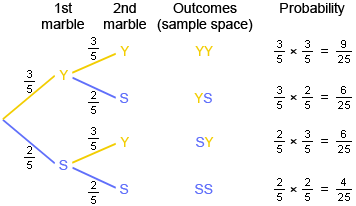
What is the probability that the marbles were both yellow?
9/25
100
Rolling a die and tossing a coin are:
- dependent events
- independent events
b. independent events
200
Sally tossed a coin 3 times and recorded the results.
What is the probability that Trial 4 will result in a tail?
Give your answer as a percentage.
50%
200
Twenty-three students were asked whether they could ride a bike or swim.
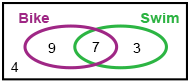
What is the probability of picking a student who can ride a bike but who cannot swim?
9/23
200
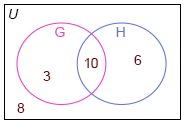
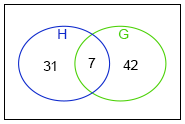
In this Venn diagram, U represents the set of outcomes of an experiment (the sample space), and G and H are two events.
The numbers show the number of outcomes in each region.
What is the probability that the event G occurs?
13/27
200
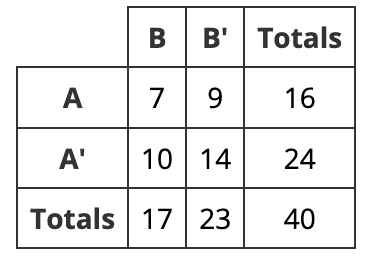
The two-way table shows the numbers of people who like or don’t like products A and B.
One person who likes product B is selected at random.
What is the probability the person also likes product A?
7/17
200
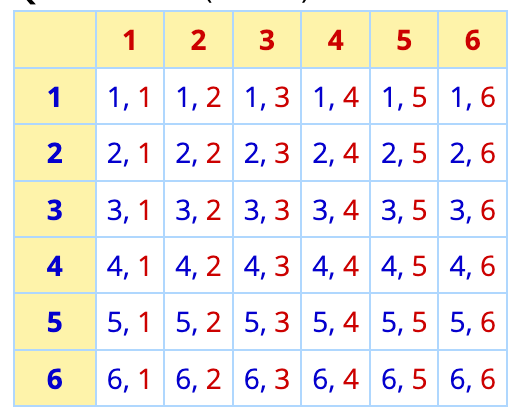
The diagram shows the possible outcomes when two dice are thrown.
How many outcomes are favourable to a 1 and a 4 in any order?
2
200
The probability tree diagram shows the outcomes and probabilities when selecting a counter from a bag of counters and then tossing two coins.
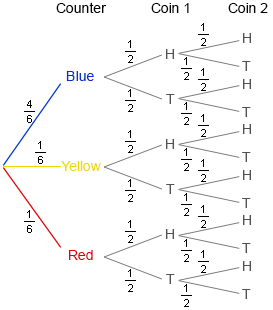
What is the probability of selecting a red counter from the bag and then tossing two heads?
1/24
200
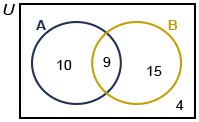
The Venn diagram shows the number of elements in events A and B. Select Pr(A):
3/5
300
When throwing two dice and adding the results, the probability of getting a sum from 2 to 12 inclusive is:
1
300
A group of people were asked if they owned a cat or a dog.
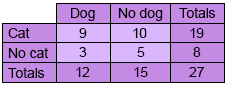
What is the probability of randomly selecting a person from this group who owns at least one pet?
22/27
300
For events A and B,
P(A) = 0.6
P(B) = 0.2
P(A ∪ B) = 0.55
∴ P(A ∩ B) =
0.25
300
For events A and B,
P(A) = 0.7
P(B) = 0.2
P(A|B) = 0.4
∴ P(A ∩ B) =
0.08
300
Jamie and Suzie each drew one card from a standard deck of 52 cards.
First Jamie drew the three of diamonds and left it face up on the table.
Then Suzie drew her card from the pack.
What is the probability that Suzie’s card is also a three?
1/17
300
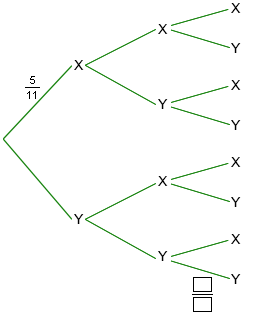
This tree diagram shows a three-step selection without replacement. What is the value of the missing probability?
4/9
300
Consider the Venn diagram below. Are the events and A and B independent?
No
400
Brown bears attempt to catch salmon. During the day, 20% of the attempts are successful. During the night, 36% of attempts are successful.
A bear tries to catch 40 fish during the day and makes 50 attempts at night.
Use probability to estimate the number of fish the bear caught.
26
400
After 70 animals were examined, it was found that 24 had neither claws nor fur, 41 had fur and 37 had claws.
If an animal chosen at random is found to have fur, what is the probability that it will also have claws?
32/41
400
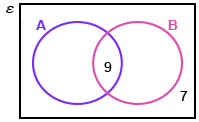
Work out the missing numbers in this Venn diagram and then find the following probabilities.
P(A|B) = 9/20
P(B|A) = 9/ 31
∴ P(A)= and P(B)=
P(A) = 31/49
P(B) = 20/49
400
A pack of twenty cards shows the whole numbers 1 to 20 inclusive, one number per card.
If two cards are drawn together at random, what is the probability that both are prime numbers?
Give your answer as a fraction in its simplest form.
14/95
400
Lana and Jess both sit a Science quiz. Lana has a 75% chance of passing the quiz and Jess has an 85% chance.
Using the tree diagram, calculate the probability that only one of them passes the quiz.
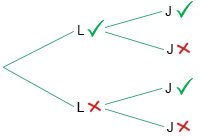
32.5%
400
A and B are two independent events such that Pr(A) = 0.45 and Pr(B) = 0.5.
Then Pr(A∪B) =
0.73