This is what collinear means.
What is points on the same line?
The first reason on any algebra proof is this ____.
Given
Point B is in between point A and point C. They are all on the same line. Therefore AB + BC = AC. What did I use to find this?
What is segment addition postulate?
What is if the non-common sides of two adjacent angles form a right angle, then the angles are complementary.
The Complement Theorem
The process of reasoning logically that uses facts. definitions, accepted properties, and laws of logic to arrive at a valid conclusion
What is Deductive Reasoning.
(If wrong -1000)
Points that lie on the same plane are said to be this.
What is coplanar?
What property is shown?
A=A
What is reflexive property?
If B is the midpoint of AC, how did I find that AB=BC
What is definition of midpoint theorem?
If <M and <N form a right angle, how do I know that they are complementary?
What is complement theorem?
Law stating that if a conditional statement is true and its hypothesis is true, then its conclusion is true.
What is Law of Detachment.
Find the midpoint of the following points.
(4,6) and (-8,1)
What is (-2, 3.5)
True or False. This would be an example of the transitive property:
If /_A+/_B=180° and /_B+/_C=180°
then
/_A=/_C
False, Congruent Supplements Theorem
True/False. Definition of congruence is only used with segment proofs.
False.
Give an example of a theorem that is used just with angles. (Having to do with angles)
What is...
Vertical Angles Theorem
Complement Theorem
Supplements Theorem
Congruent Supplements Theorem
Congruent Complements Theorem
Find contrapositive of the following statement and determine if it is True or False:
If a triangle has a right angle, then it is a right angle.
What is if a triangle is not a right angle, then it does not have a right angle. T
What is the midpoint formula?
(x1 + x2)/(2),(y1 + y2)/(2)
What is the last reason for the following algebra proof? (Hint, may be more than one answer.)
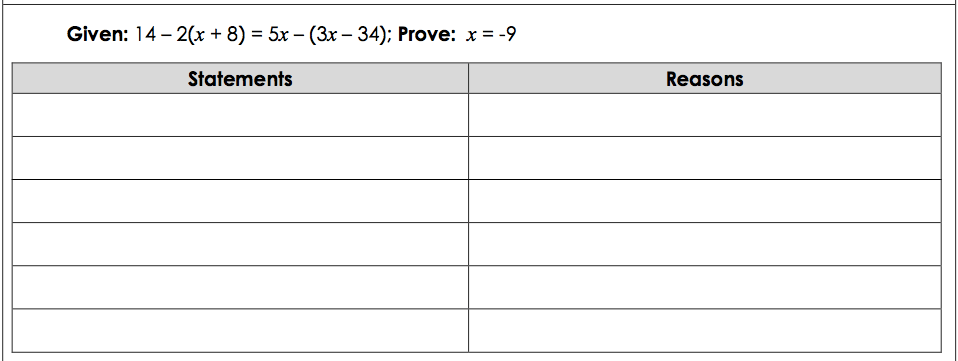
What is the division or symmetric property?
What is reason 4 is the proof?
HINT: Look at the Givens.

What is the definition of midpoint?
(Midpoint Theorem)
If <X is supplementary to <Y and <X is supplementary to <Z, then <Y is congruent to <Z.
What did I use to find out that <Y is congruent to <Z
What is congruent supplements theorem?
Find the definition of a conditional statement and identify its two parts, what is the symbolic notation for each?
What is...
Conditional Statement: a logical statement in "if, then" form.
Two Parts: Hypothesis and Conclusion
Symbolic Notation: p and q
Find the distance between these two points:
(-7,-4) and (-11,-8)
sqrt(32) or 5.7
What are the 4 steps to this proof? (Most Efficient)
Given: 4x-10=7-2x
Prove: x=17/6
What is...
1) Given
2) Add POE
3) Add POE
4) Division POE
What is the 5th statement for the proof?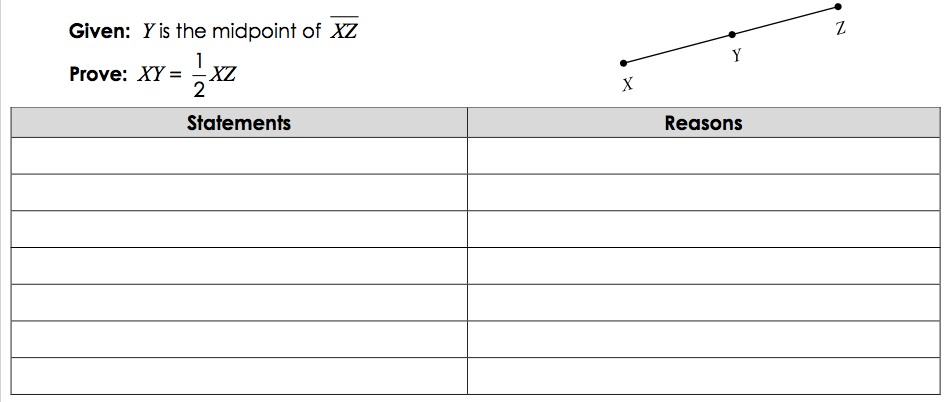
What is 2xy = xz?
What are the 6 steps to this proof?
Given: ∠ABC and ∠CBD form a linear pair. m∠ABC= 5x and m∠CBD= 4x
Proof: x=20
What is...
1) Given:
2) Supplement Theorem
3) Definition of Supplementary Angles
4) Substitution
5) Simplify
6) Division POC
Write an inverse, biconditional, contrapositive and converse of this statement. Determine if each statement is true or false, if false give a counter example
OS: If you studied for the test that will be on Wednesday, you will pass
Inverse: "If you did not study for the test that will be on Wednesday, you will not pass."
False: EX: you got lucky or are just big brain.
Biconditional: "You will pass if and only if you studied for the test that will be on Wednesday."
False: EX: you got lucky or just remembered everything from class (or dare I say cheated).
Contrapositive: "If you won't pass, you didn't study for the test that will be on Wednesday."
False: EX: You studied, but studied the wrong content, or didn't study enough.
Converse: "If you will pass, you studied for the test that will be on Wednesday.
False: EX: Should be true but not always.