Graphing Proportional Relationships
Proportional Relationship Equations
Identifying Proportional Relationships
Proportional Relationship Problems
Proportion Word Problems
100
What is the ordered pair for the origin?
(0,0)
100
Is the equation y = 3x proportional? Explain.
Yes. The equation is in the form of y = kx, where k = 3.
100
Are the ratios below proportional? Explain.
3/4 and 9/12
Yes. If you multiply 3/4 by 3/3 you get 9/12.
100
The triangles below are similar. What is the value of x?
x = 5
100
According to the scale on a map, 4 cm on the map equals 32 miles. How many centimeters on the map would represent 384 miles?
48 cm
200
How do you tell if a graph represents a proportional relationship?
The graph is a straight line that passes through the origin.
200
Is the equation y = 4x + 10 proportional? Explain.
No. The equation is NOT in the form of y = kx.
200
Does the graph below represent a proportional relationship? Explain.
No. Although the graph is a straight line, it does not pass through the origin.
200
Find the value of n in the proportion above.
n = 3.8
200
Bob ran 66 miles in 12 hours. How many miles did Bob run per hour?
5.5 miles per hour
300
Does every straight line graph represent a proportional relationship? Explain.
No. The graph would have to be a straight line AND pass through the origin.
300
What is the constant of proportionality in the equation below?
y= ¾ x
k = ¾
300
Does the table below represent a proportional relationship? Explain.
No. There is no constant multiplier AND (0, 0) would not make sense in the table.
300
The table below is proportional. Find the constant of proportionality.
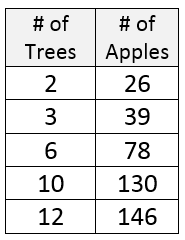
k = 13
300
The scale factor for a model airplane to a real airplane is 1 in : 9ft. What would the length of the model plane be if the real plane is a 198 feet?
22 inches
400
Does this graph represent a proportional relationship? Explain.
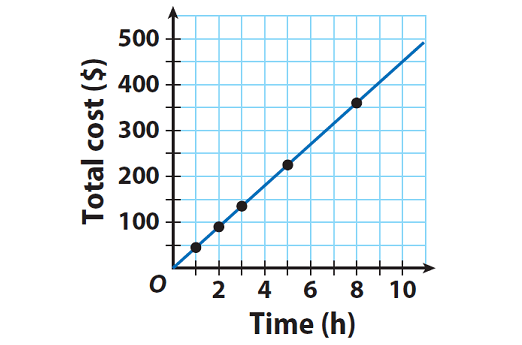
Yes. It is a straight line that passes through the origin.
400
The constant of proportionality for the graph below is 1/6. What is the equation?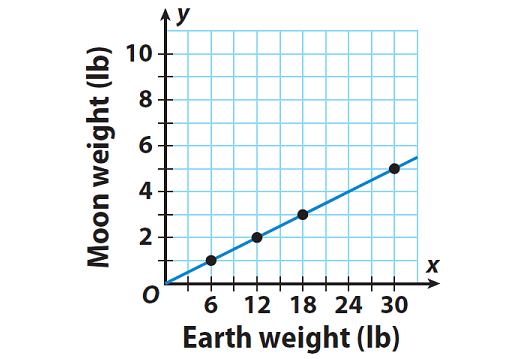 
y = 1/6x
400
Does the table below represent a proportional relationship? Explain.
Yes. The constant of proportionality is 9 AND (0, 0) makes sense in the table.
400
The constant of proportionality is 3. Write an equation for the proportional relationship.
y = 3x
400
Steve’s car used 38 gallons of gasoline to go 912 miles. At that rate, how many gallons would be used to go 2736 miles?
114 gallons
500
Paul plots the following points on a graph.
(0, 0), (1, 3), (2, 7), and (3, 15)
Do his points represent a proportional relationship? Explain.
No. Although (0, 0) is a point on the graph, the points do not form a straight line.
500
Write an equation for the proportional relationship shown in the table below.
y = 3/2 x OR y = 1.5x
500
Are the ratios below proportional? Explain.
2/5 and 4/7
No. To get from 2 to 4, you multiply by 2. However, 5 multiplied by 2 is not 7.
500
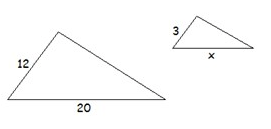
The triangles below are similar. What is the value of x?
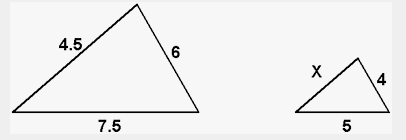
x = 3
500
Sam took 8 hours to drive 272 miles. What was the unit rate in miles per hour?
34 mph