Domains & Ranges
Linear Functions
Exponential Functions
Composition of Functions
Logarithmic Functions
Powers, Polynomials, and Rational Functions
The Unit Circle
100
Suppose f(x) = x^2. What is the domain of f ? What is the range of f ?
Domain of f: the set of all real numbers \mathbb{R}
Range of f: the set of all non-negative, real numbers {x\in \mathbb{R} | x\geq 0}
100
What is the slope of the following line? What is its y-intercept?
y = \frac{2}{5}x+3
\text{slope }m = \frac{2}{5}
y\text{-intercept }b = 3
100
For which pairs of consecutive points int he following figure is the function graphed: increasing & concave up, increasing & concave down, decreasing & concave up, and decreasing & concave down?
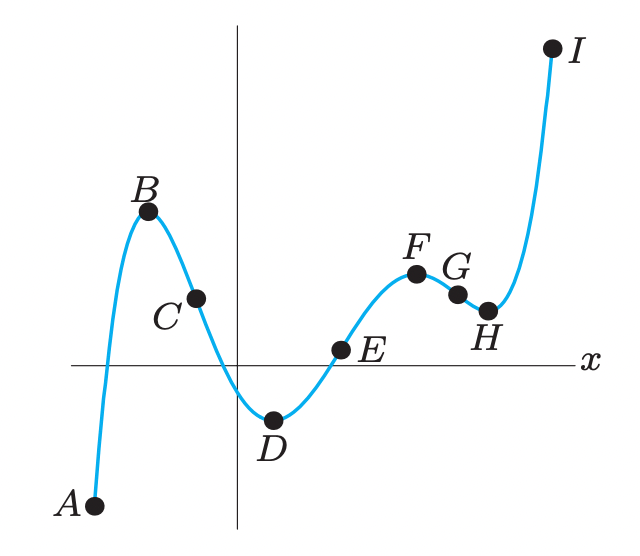
Increasing & CU: (D,E), (H,I)
Increasing & CD: (A,B), (E,F)
Decreasing & CU: (C,D), (G,H)
Decreasing & CD: (B,C), (F,G)
100
Describe the steps you need to do to compute f(g(1)) for any functions f(x) and g(x).
(1) Compute g(1)
(2) Note that g(1) represents some number. We plug this number into f(x) to get f(g(1))
100
Completely simplify the expression
5e^{\ln(a^2)}
5a^2
100
Determine the end behavior of the following function as x approaches positive infinity and as x approaches negative infinity.
f(x) = -10x^5
\text{As }x\rightarrow +\infty, f(x)\rightarrow -\infty
\text{As }x\rightarrow -\infty, f(x)\rightarrow +\infty
100
\text{Find the exact values of}\cos(0) and \sin(0).
cos(0)=1, sin(0)=0
200
Give the approximate domain and range of the following function. Assume the entire graph is shown.
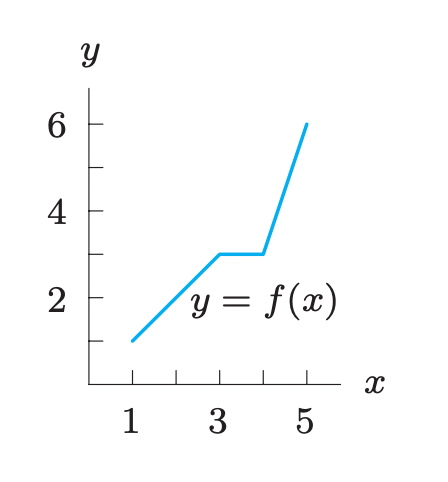
Domain of f is {x\in \mathbb{R} | 1 \leq x \leq 5}
Range of f is {x\in \mathbb{R} | 1 \leq x \leq 6}
200
Determine the slope and y-intercept of the line whose equation is
7y+12x-2=0
\text{slope }m=-\frac{12}{7}
y\text{-intercept }b= \frac{2}{7}
200
Consider the following exponential growth function, where P is a population (in thousands) and t is a unit of time. What is the initial population? What is the growth rate?
P=3.2e^{0.03t}
P_0=3.2 \text{ (3200 people) }
a=e^{0.03} \text{ (~3% increase per unit of time)}
200
Compute f(g(1))\text{ and }g(f(1)) given the following functions
f(x)=sqrt(x+4)\text{ and }g(x)=x^2
f(g(1))=sqrt5
g(f(1))=5
200
Completely simplify the expression
\ln(1/e) + \ln(ab)
\ln(a)+\ln(b)-1
200
Determine the end behavior of the following function as x approaches positive infinity and as x approaches negative infinity.
f(x)=e^x
\text{As }x\rightarrow +\infty, f(x)\rightarrow +\infty
\text{As }x\rightarrow -\infty, f(x)\rightarrow 0
200
Convert the following radians into degrees
\text{(a) } \frac{3\pi}{2}
\text{(b) } \frac{5\pi}{3}
\text{(a) } \frac{3\pi}{2} = 270 \text{ degrees}
\text{(b) } \frac{5\pi}{3} = 300 \text{ degrees}
300
Find the domain and range of
\frac{1}{x^2+2}
Domain is \mathbb{R}
Range is {y\in \mathbb{R} | 0 < y \leq \frac{1}{2}}
300
Find the equation for the line that passes through the points (-1,0) and (2,6).
y=2x+2
300
Consider the following exponential functions. Which represent exponential growth and which represent exponential decay?
\text{(a) }P=15e^{0.25t}
\text{(b) }P=e^{0.2t}
\text{(c) }P=2e^{-0.5t}
\text{(d) }P=7e^{-\pi t}
(a) and (c) are exponential growth functions
(b) and (d) are exponential decay functions
300
Compute f(g(x)),\text{ }g(f(x)), and f(x)g(x) if f(x)=1/x, g(x)=3x+4
f(g(x)) = 1/(3x+4)
g(f(x)) = 3/x + 4
f(x)g(x) = (3x+4)/x
300
Solve for x.
2x-1=e^{\ln(x^2)}
x=1
300
Determine the end behavior of the following function as x approaches positive infinity and x approaches negative infinity.
f(x)=\frac{6+5x-3x^2}{x^2-4}
\text{There is a horizontal asymptote at }y=-3.
300
Find point P and the indicated angle \theta.
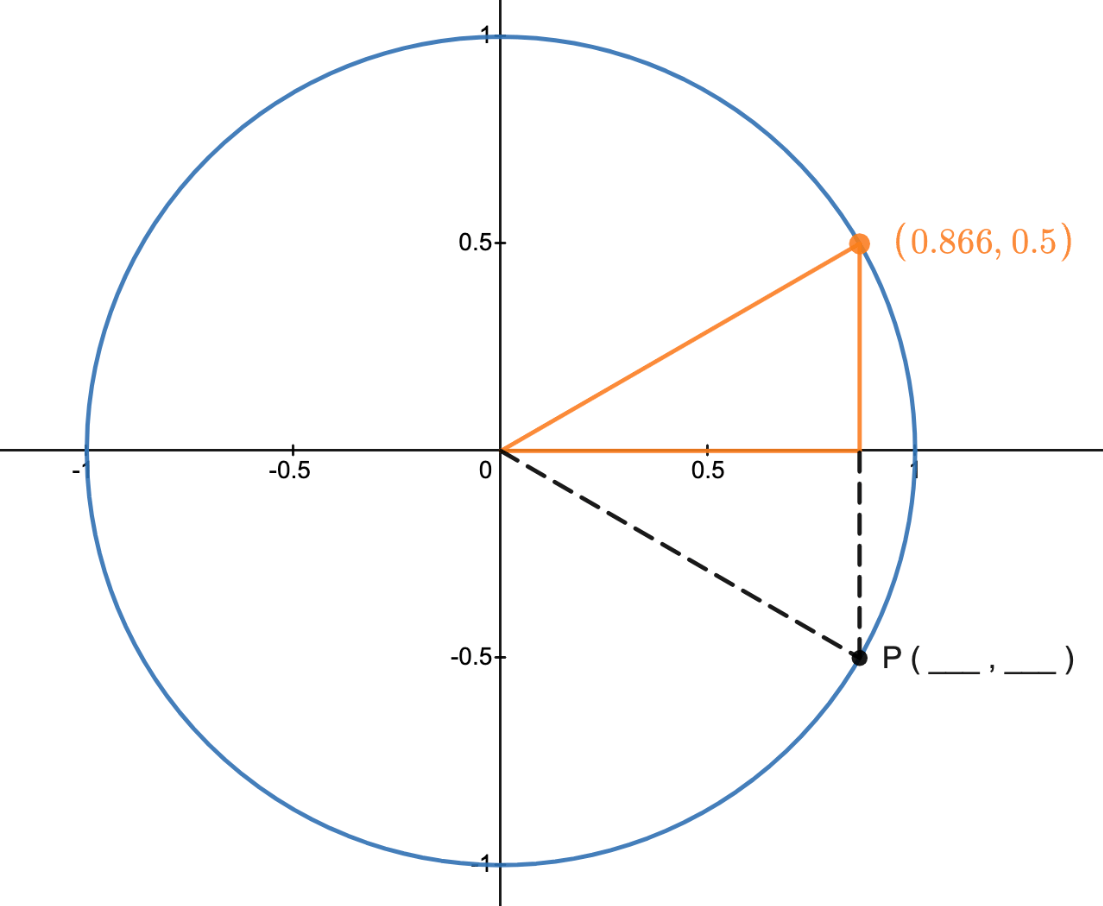
\text{Point }P=(\frac{\sqrt(3)}{2},-\frac{1}{2})
\text{Angle }\theta=\frac{\pi}{6} \text{ or }30\text{ degrees}
400
Find all values of t for which f(t) is a real number. Then solve for f(t) = 3.
f(t) = sqrt{t^2-16}
f(t)\text{ is real when }t\leq -4\text{ or }t\geq 4
t= pm5
400
Match the graphs below with the following equations. Note that graphs may not be drawn to scale.
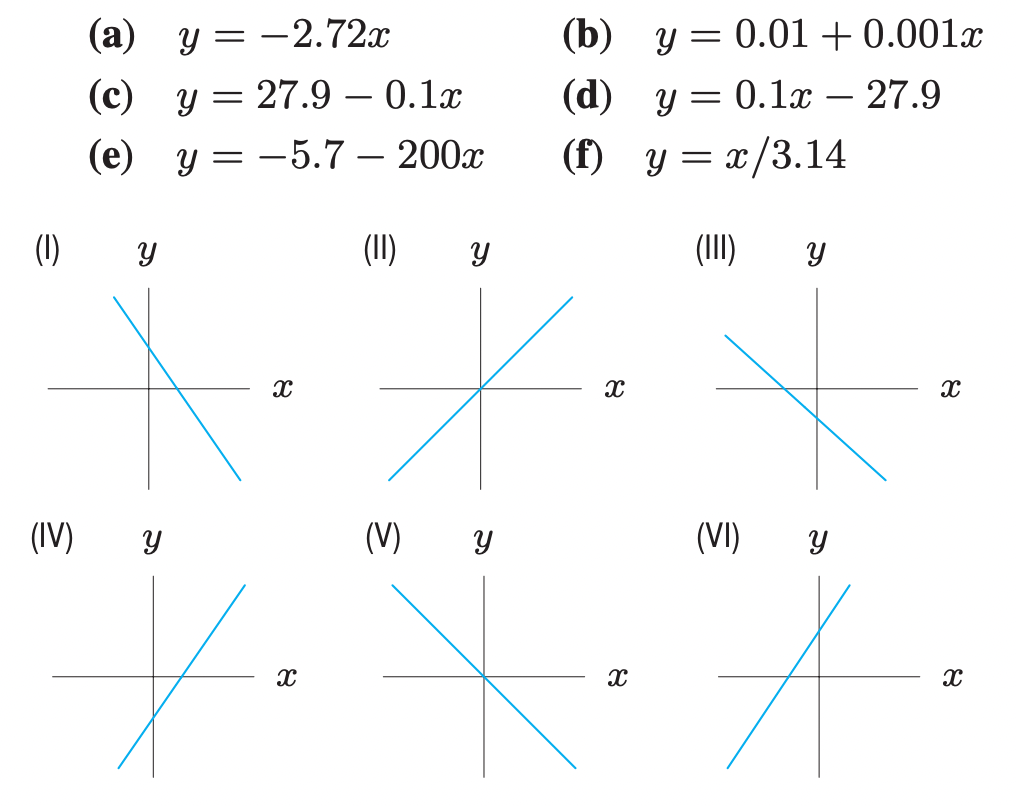
(a) = graph (V)
(b) = graph (VI)
(c) = graph (I)
(d) = graph (IV)
(e) = graph (III)
(f) = graph (II)
400
A town has a population of 1000 people at time t = 0. Write a formula for the population, P, of the town as a function of year t, if
(1) the population increases by 50 people each year
(2) the population increases by 5% each year.
Explain how they are different.
\text{(1) Formula for increase of 50 each year: }P=1000+5t
\text{(2) Formula for increase of 5% each year: }P=1000(1.05)^t
\text{(1) is linear growth and (2) is exponential growth}
400
If f(x)=x^2+3 , find and simplify f(t^2+1) and (f(t))^2+1 .
f(t^2+1) = t^4 + 2t^2 + 4
(f(t))^2+1 = t^4 + 6t^2 + 10
400
Solve for x.
7^{x+2}=e^{17x}
x=\frac{-2\ln(7)}{\ln(7)-17}
400
Find a cubic polynomial for the following graph.
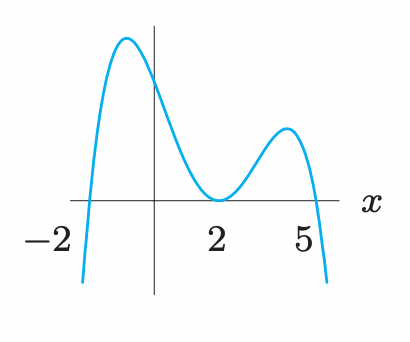
f(x)=(x+2)(x-2)(x-5)
400
Find the indicated angle using the following image of the unit circle.
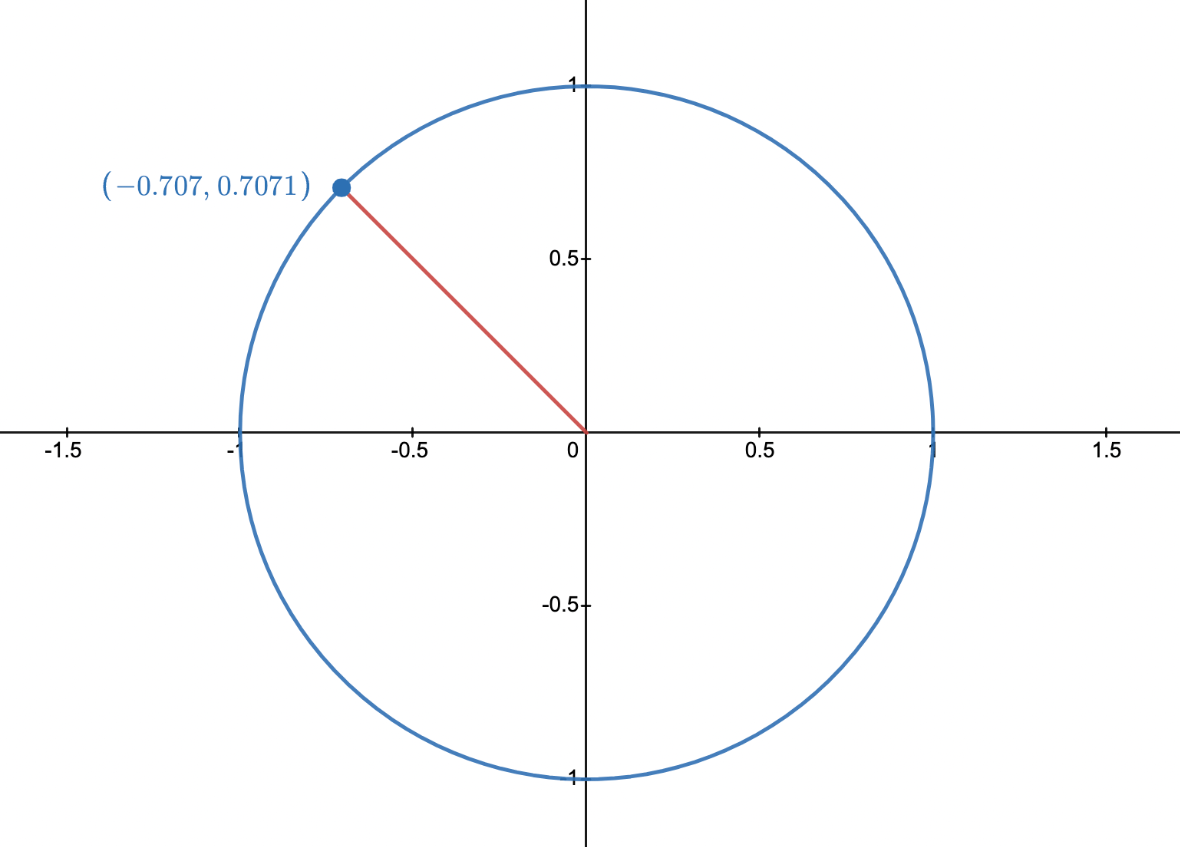
\theta=\frac{3\pi}{4}\text{ or }135 \text{ degrees}
500
Which of the following functions has its domain identical with its range?
f(x) = x^2,\text{ } g(x) = sqrt(x)
h(x)=x^3,\text{ } i(x) = |x|
\text{Domain and range of }g(x)\text{ is }{x\in \mathbb{R} | x\geq 0}
\text{Domain and range of }h(x)\text{ is }\mathbb{R}
500
Find equations for the lines through the point (1,5) that are parallel to and perpendicular to the line with equation y+4x=7.
\text{Parallel line: }y=-4x+9
\text{Perpendicular line: }y=\frac{1}{4}x+\frac{19}(4}
500
In 2010, the world's population reached 6.91 billion and was increasing at a rate of 1.1% per year. Assume that the growth rate remained constant.
\text{(a) Write a formula for the world population (in billions) as}
\text{a function of the number of years since 2010.}
\text{(b) Using the formula from (a), estimate the population of the world in 2020}
\text{(c) The current world population is ~7.87 billion.}
\text{How does this different from the estimate in (b)?}
\text{What does this mean for the growth rate?}
\text{(a) }P=6.91(1.01)^t
\text{(b) }P(11) = 6.91(1.01)^{11} = 7.79 \text{ (7.79 billion people)}
\text{(c) Because the actual population > estimated population, the growth rate must have increased since 2010.}
500
If g(x)=x^2-2x+1 , compute the following
\frac{g(1+h)-g(1)}{h}
h
500
Solve for x.
4e^{2x-3}-5=e
x=\frac{\ln(e+5)-\ln(4)+3}{2}
500
Find all horizontal and vertical asymptotes for the following rational function
f(x)=\frac{x^2+5x+4}{x^2-4}
\text{There are vertical asymptotes at }x=\pm2
\text{There is a horizontal asymptote at }y=1
500
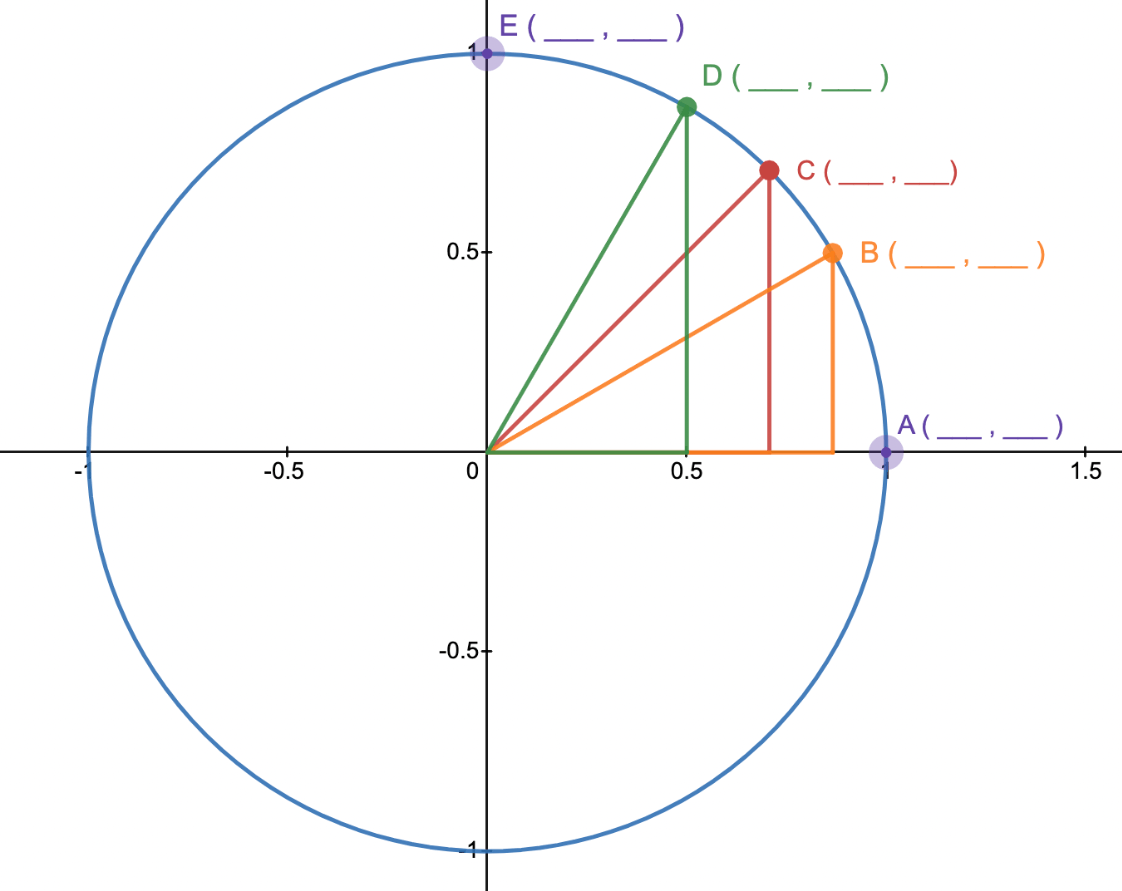
Fill out the first quadrant of the unit circle.
