SEGMENTS
ANGLES
TRANSVERSAL
100
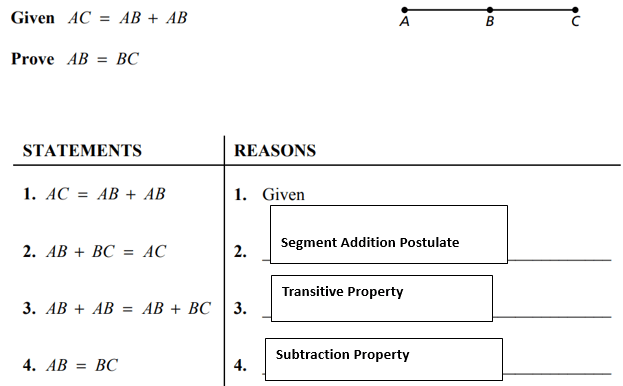
What property(s) would justify the following conclusion
If AB + BC = EF + FG and AB + BC = AC, then EF + FG = AC
Transitive Property or Substitution Property
100
Find the measure of angle b and state by which theorem
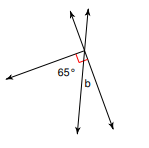
Since we see there is a red box angle
Complement theorem: these angles add up to 90
b + 65 = 90
b = 25
100
What type of angle pairs are <2 with <8 and <1 with <7?
Alternate Exterior Angles :)
They are opposite sides of the transversal (the middle line) and outside of the two lines
200
If M is the midpoint of AM and AM is 2x and B is 12.
What is the measurement of AM?
2x = 12
x = 6
AM = 2(6)
AM = 12
200
X and Y are supplementary angles. If angle X = 3a + 4 degrees and angle Y = 2a -9 degrees, what is the value of a?
Supplementary means they add up to 180
X + Y = 180
(3a + 4) + (2a - 9) = 180
5a -5 = 180
5a = 185
a = 37
200
The following are parallel lines intersected by a transversal.
Name 2 pairs of angles that are supplementary and 2 pair of angles that are congruent and label what type of angles they are (4 pairs total)
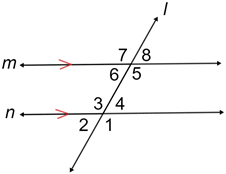
Supplementary:
Consecutive Interior Angles: <5 and <4
Linear Pair: <7 and <8
Consecutive Exterior Angles: <8 and <1
Congruent:
Corresponding Angles: < 7 and <3
Alternate Exterior Angles: <8 and <2
Alternate Interior Angles: <6 and <4
300
300
Name two pairs of angles that are supplementary and complementary (4 pairs total)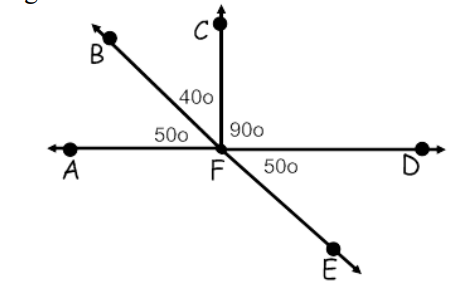
Complementary:
<AFB and <CFB
<CFB and <DFE
Supplementary:
<CFD and <CFA
<BFD and <DFE
300
These are parallel lines intersected by a transversal. Find the value of x and state by which theorem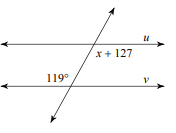
Alternate Interior Angles Theorem: alternate interior angles are congruent
x + 127 = 119
x = -8
400
Points A, B and C are collinear. Point B is between A and C. Solve for x, 𝐴𝐶 = 3𝑥 + 3, 𝐴𝐵 = −1 + 2𝑥, 𝐵𝐶 = 11
AB + BC = AC
(-1 + 2x) + (11) = (3x + 3)
2x + 10 = 3x + 3
10 = x + 3
x = 7
400
Find the value of x and state by which theorem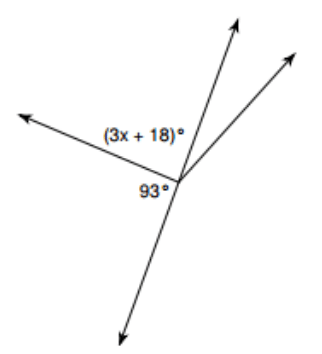
Supplement theorem: linear pairs add up to 180
(3x + 18) + (93) = 180
3x + 111 = 180
3x = 69
x = 23
400
These are parallel lines intersected by two transversals.
Find b and state by which theorem.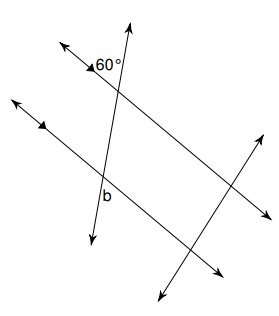
Alternate Exterior Angles Theorem: alternate exterior angles are congruent
b = 60