Resilience
Gratitude
Perseverance
Endurance
100
What kind of system of equations does the graph display below?
No Solution
100
What method would you use to solve this system of equations algebraically?
2x + y = 1
y = 2x + 1
Substitution
100
What's the constant of proportionality for this graph? (Make sure to include UNITS!)
37.5m/g
100
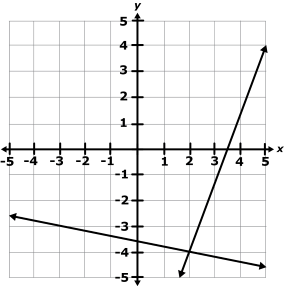
This graph is an example of what kind of system of equations?
One Solution
200
What is the y coordinate for the point of intersection displayed on the graph?
-4
200
What is the equation of the line in slope-intercept form?
y = -3/2x + 3
200
Solve for r.
r = -1
200
What is the equation of the line in the graph below in slope-intercept form?
y = 8/3x + 4
300
Solve the system of equations.
x - y = 3
7x - y = -3
(-1, -4)
300
Justin’s pay is represented by this line graph.
Molly’s pay is represented by the equation y = 9x. Who makes more money and by how much?
A. Justin earns $2 more per hour than Molly.
B. Justin earns $3 more per hour than Molly.
C. Molly earns $2 more per hour than Justin.
D. Molly earns $1 more per hour than Justin.
Justin makes $7/hour
C. Molly earns $2 more per hour than Justin.
300
Solve the system of equations.
4x+5y=9
3x-3y=0
(1, 1)
300
Here is information about the cost of carpet at two stores.
Carpet Store A is represented by the graph.
Carpet Store B sells 100 square yards of carpet for $1750.
What is the cost, per square yard, of the carpet at the store with the lesser cost?
Carpet Store A: $15.sq. yd.
400
Solve for p.
p = 1
400
What is the solution to this system of equations?
8x - 6y = -20
-16x + 7y = 30
(-1, 2)
400
Solve for v.
v = -1
400
What is the solution to this system of equations?
4x-2y=14
10x+7y=-25
(1, -5)
500
Yomaira and Kevin play a game in which they earn the same number of points for each goal and lose the same number of points for each penalty.
• Yolanda makes 6 goals and 3 penalties, ending the game with 6 points.
• Neel earns 8 goals and 9 penalties, and ends the game with -22 points.
Write a system of equations that describes Yolanda's and Neel's outcomes.
**Remember**
- Define your variables first
- Then setup your equations based off the problem
- Lastly, solve for the solution
x=points for each goal
y=points for each penalty
6x+3y=6
8x+9y=-22
Solution: (4, -6)
Each goal earns 4 points. Each penalty loses 6 points.
500
What is the solution to the system of equations below?
7x + 8/7y = 4
3x - 5/7y = 27
(4, -21)
500
Jamia babysits for two different families. One family pays her $6 each hour and a bonus of $20 at the end of the night. The other family pays her $5 per hour and a bonus of $30 at the end of the night.
**Remember**
- Define your variables first
- Then setup your equations based off the problem
- Lastly, solve for the solution
x = # of hours babysitting
y = total amount of money paid after babysitting
6x + 20 = y
4x + 30 = y
(5, 50)
500
Solve the systems of equations below.
4x - 3/4y = 9
7x + 2/4y= -6
(0, -12)