Resilience
Gratitude
Perseverance
Endurance
100
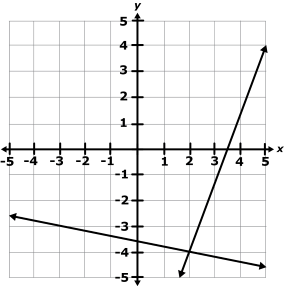
What kind of system of equations does the graph below display?
No Solution
100
True or False:
This equation matches the line on the graph?
y = 3/2x + 1
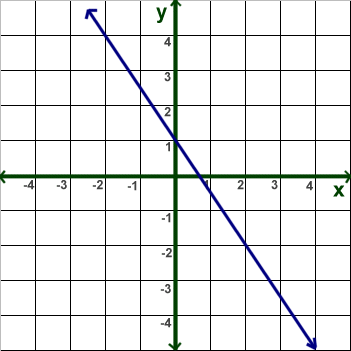
False
Equation should be: y = -3/2x + 1
100
Jeremy rides his bike at a rate of 12 miles per hour. Below is a table that represents the number of hours
and miles Kevin rides. Assume both bikers ride at a constant rate. How fast does Kevin ride his bike?
Time in Hours (x) / Distance in Miles (y)
1.5 / 17.25
2 / 23
3.5 / 40.25
4 / 46
11.5 miles per hour
100
This graph is an example of what kind of system of equations?
One Solution
200
What are the coordinates of the point of intersection to this system of equations?
(2, -4)
200
What is the equation of the line on the coordinate plane shown?
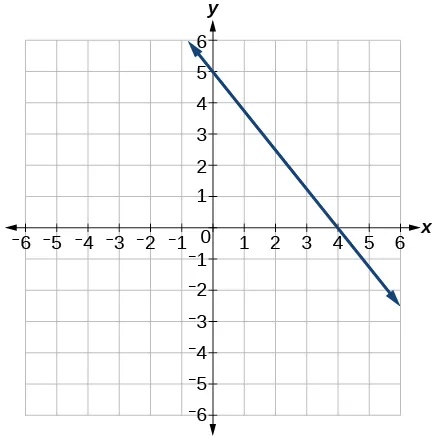
y = -5/4x + 5
200
Solve for r.
r = -1
200
What is the equation of the line in the graph below in slope-intercept form?
y = 8/3x + 4
300
Solve the system of equations.
x - y = 3
7x - y = -3
(-1, -4)
300
Which sequence of transformations occurred to turn Triangle 1 into Triangle 2?
A. Reflection across the x-axis followed by a translation
B. 180 degree rotation
C. 90 degree counterclockwise rotation about the origin
D. 90 degree clockwise rotation about the origin
D
300
Solve the system of equations.
4x+5y=9
3x-3y=0
(1, 1)
300
Triangles PQR and P′Q′R′ are shown on a coordinate plane.
Describe the following sequence of transformations that created Triangle P'Q'R' from Triangle PQR?
A reflection across the y-axis followed by a 14 unit translation up
400
Solve for x.
-15x + 24 + 16x = 3x - 24
x = 24
400
What is the solution to this system of equations?
8x - 6y = -20
-16x + 7y = 30
(-1, 2)
400
What value of v will make this equation true?
v = -1
400
What is the solution to this system of equations?
4x-2y=14
10x+7y=-25
(1, -5)
500
Eddie and Sha'heem play a game in which they earn the same number of points for each goal and lose the same number of points for each penalty.
• Eddie makes 6 goals and 3 penalties, ending the game with 6 points.
• Sha'heem earns 8 goals and 9 penalties, and ends the game with -22 points.
Write and solve the system of equations that describes Eddie's and Sha'heem's outcomes.
**Remember**
- Define your variables first
- Then setup your equations based off the problem
- Lastly, solve for the solution
x=points for each goal
y=points for each penalty
6x+3y=6
8x+9y=-22
Solution: (4, -6)
Each goal earns 4 points. Each penalty loses 6 points.
500
Use substitution to solve the system of equations. Show work and give answer as and order pair.
8x + 6y = 26
y= 2x + 1
(6, 13)
500
Faith babysits for two different families. One family pays her $6 each hour and a bonus of $20 at the end of the night. The other family pays her $5 per hour and a bonus of $30 at the end of the night.
**Remember**
- Define your variables first
- Then setup your equations based off the problem
- Lastly, solve for the solution
x = # of hours babysitting
y = total amount of money paid after babysitting
6x + 20 = y
4x + 30 = y
(5, 50)
500
Here is information about the cost of carpet at two stores.
Carpet Store A is represented by the graph.
Carpet Store B sells 100 square yards of carpet for $1750.
What is the cost, per square yard, of each carpet store?
Which carpet store has the cheaper cost? By how much?
Carpet Store A: $15.sq.yd
Carpet Store B: $17.50.sq.yd
Carpet Store A is the cheapest of the two stores