Translations and Reflections
Vertex to General Form
All About the Vertex
Domain and Range
100
The way a function moves when you change k in y=a(x-h)^2+k .
What is up or down?
100
The name for this formula:
y=a(x-h)^2+k
.
What is vertex form?
100
The highest (if it opens down) or lowest (if it opens up) point on a parabola.
What is a vertex?
100
The variable that goes with domain.
What is
x
?
200
The way a function moves when you change h in y=a(x-h)^2+k .
What is left or right?
200
The formula for general/standard form.
What is
y=ax^2+bx+c
?
200
The two letters that replace (x,y) for the coordinate point of a vertex (in their proper order).
What are
(h,k)
?
200
The variable that goes with range.
What is
y
?
300
The direction the graph of y=(x)^2 moves when you change it to y=(x+5)^2.
What is left 5?
300
The first step to changing this to general form:
y=(x-2)^2+4
What is the box method?
OR
What is multiply
(x-2)(x-2)
300
The vertex of the following:
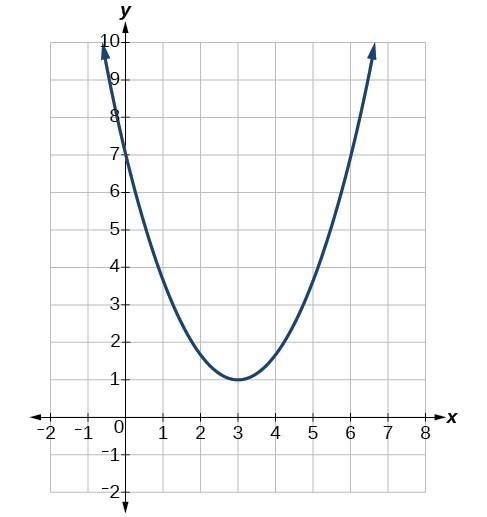
What is
(3,1)
?
300
The color of the graph of the function with the range -infty<y<=4
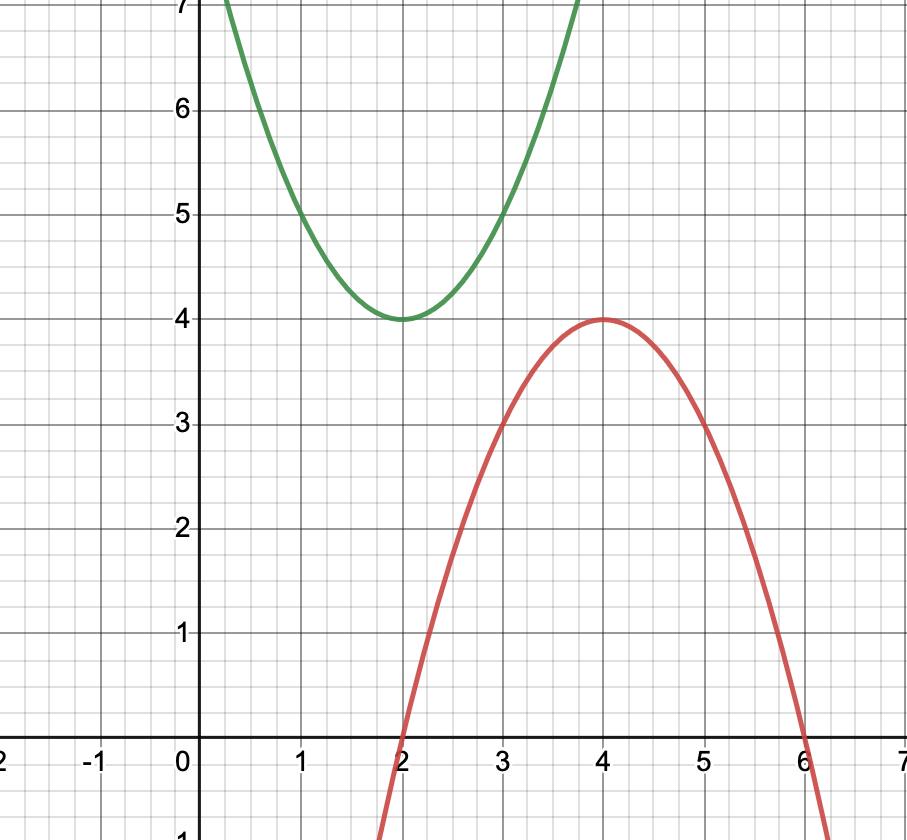
What is red?
400
How to make the graph of y=x^2 look like y=3(x)^2.
What is multiply all the y values by 3?
400
The name of the property used in step 3 in converting to general form:
Step 1:
y=5(x-3)^2+7
Step 2:
y=5(x^2-6x+9)+7
Step 3:
y=5x^2-30x+45+7
What is the distributive property?
400
The vertex of the following:
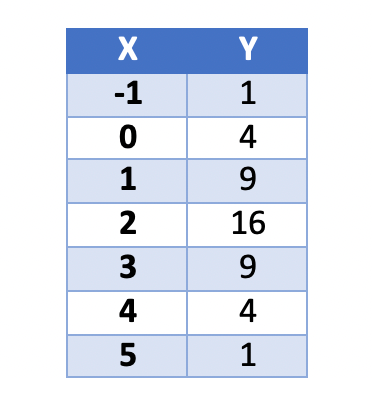
What is
(2,16)
?
400
The domain of the red line:
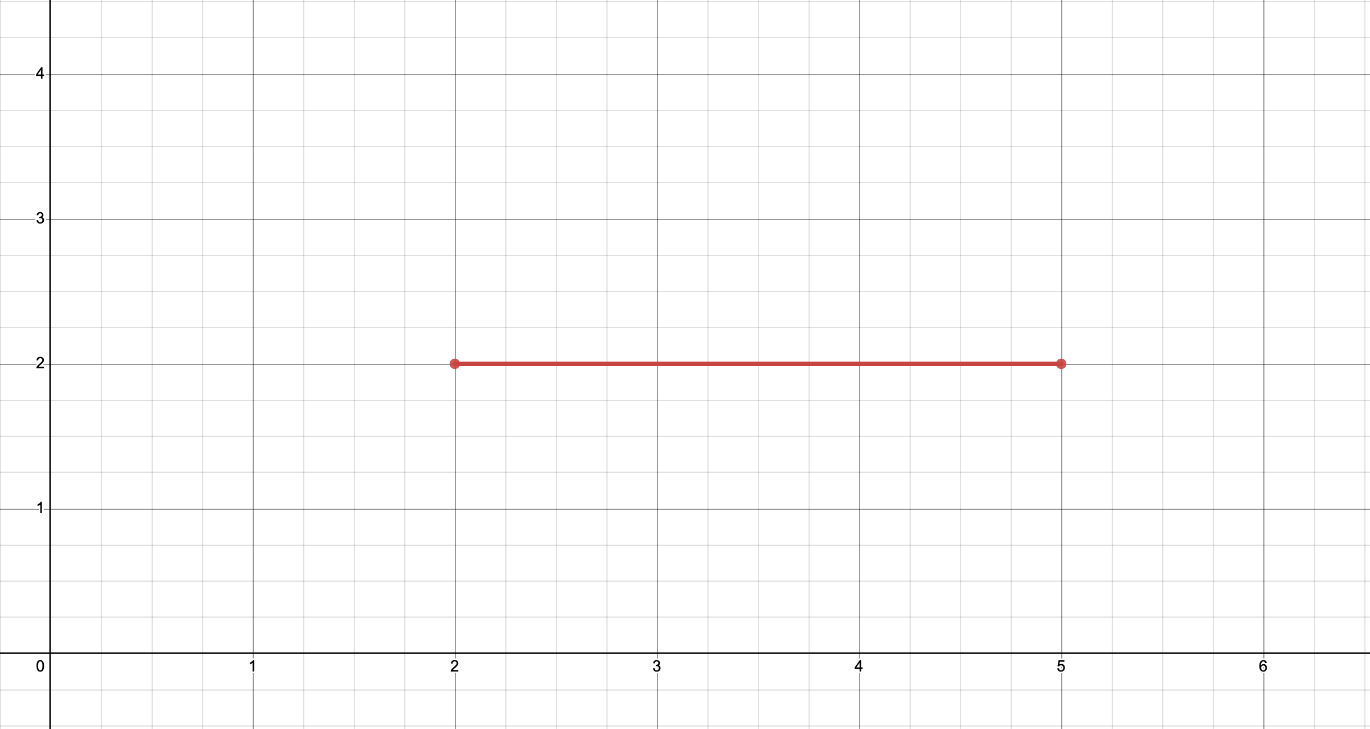
What is
2<=x<=5
?
500
The function that gives the graph:
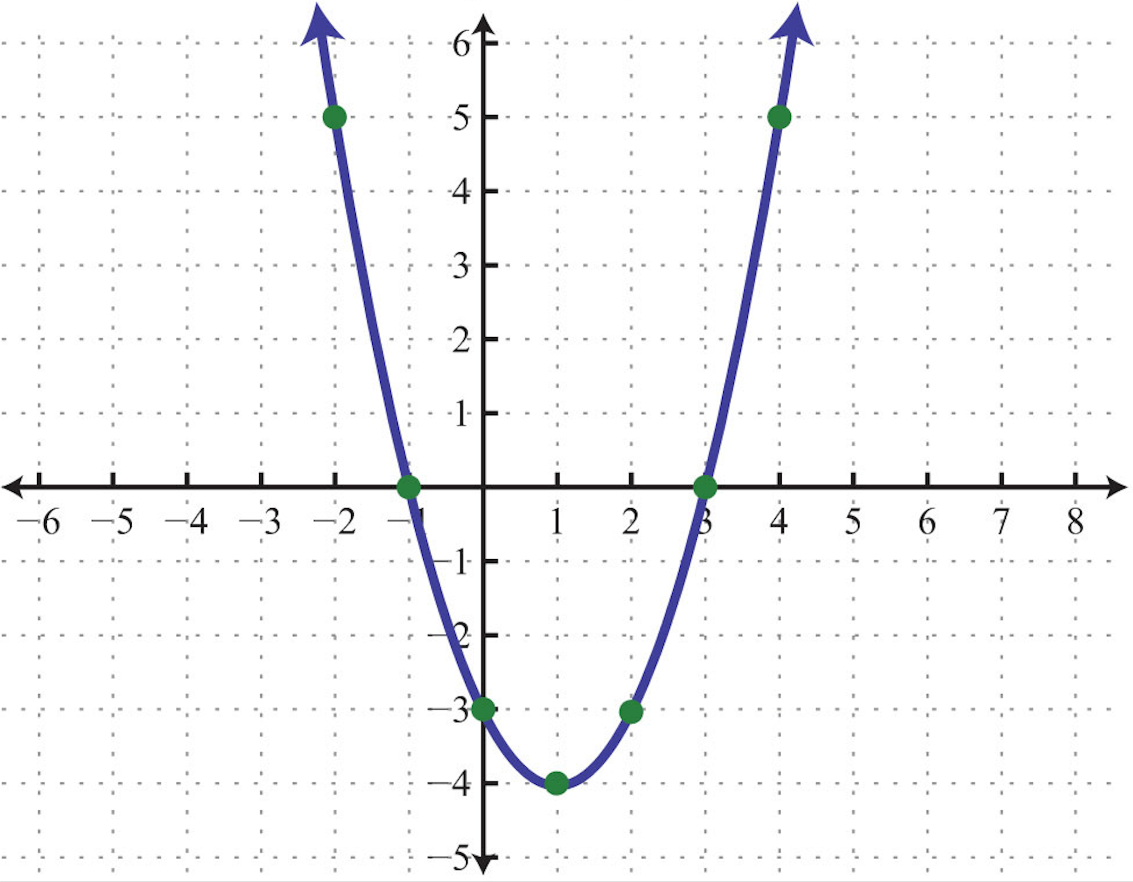
What is
y=(x-1)^2-4
?
500
y=4(x+2)^2-6 in general form.
What is
y=4x^2+16x+10
?
500
The vertex of y=5(x+3)^2-6.
What is
(-3,-6)
?
500
The range and domain of the ENTIRE parabola whose partial graph is shown:
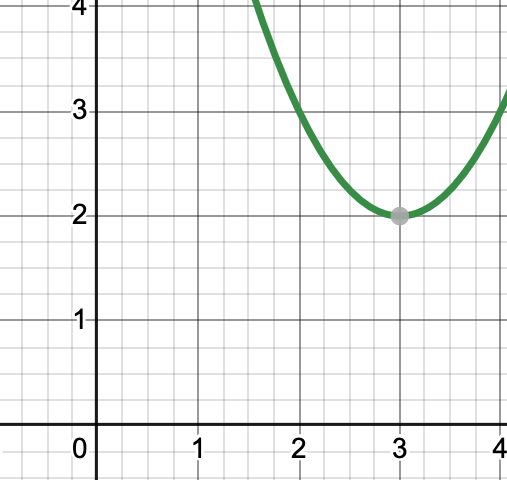
What is
-infty<x<infty
and
2<y<infty