2.1 Transformations
2.2 Characteristics (Vertex Form)
2.2 Characteristics (Standard Form)
2.2 Characteristics (Intercept Form)
2.4 Modeling
100
Write an equation g(x) that is vertical stretch by a factor of 3 and horizontal shift right 2 of the quadratic parent function
g(x) = 3(x-2)^2
100
What is a vertex?
The maximum or minimum of a quadratic function
100
What key point does standard form explicitly give you?
The y-intercept
100
What key point(s) does intercept form explicitly give you?
The x-intercepts
100
A baseball is hit into the air and its path is modeled by the function h(t) where t represents time in seconds and h represents the height of the baseball in ft. What is the height of the baseball after 6 seconds?
h(t) = -3t^2+18t+1
1 ft
200
Describe the transformations of
f(x)=x^2
represented by
g(x) = -0.5x^2-3
Vertical shrink by a factor of 1/2, reflection over the x-axis, shift down 3 units
200
Name the vertex:
f(x) = 2(x-3)^2+1
(3, 1)
200
Name the y-intercept as an ordered pair:
f(x) = -2x^2+3x-7
(0, -7)
200
Name the x-intercepts as ordered pairs:
f(x) = 2(x-3)(x+4)
(3, 0) and (-4, 0)
200
Find a quadratic function that crosses through (9, 0), (1, 0), and (0, −18)
f(x) = -2(x-1)(x-9)
300
Write an equation to model the following graph: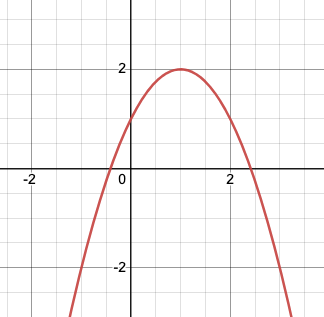
f(x) = -(x-1)^2 + 2
300
Name the axis of symmertry:
f(x) = -(x+1)^2-3
x=-1
300
Find the vertex:
f(x) = 2x^2-4x+3
(1, 1)
300
Find the vertex:
f(x) = 2(x-3)(x+3)
(0, -18)
300
Find a quadratic function that passes through (−7, −15) and has vertex (−5, 9)
f(x)=-6(x+5)^2+9
400
Given
f(x) = x^2 + 3
Write an equation for g(x) given it is a translation 1 unit left, followed by a vertical stretch by a factor of 2, followed by a reflection in the x-axis of the function f
g(x) = -2(x+1)^2 - 6
400
Graph
f(x) = 2(x-1)^2+3
*You must have at least 3 points.
400
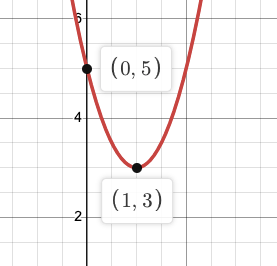
Expand to standard form:
f(x) = -3(x-1)^2+3
f(x) = -3x^2+6x
400
Is
f(x) = 2(x-2)^2
considered intercept form? Why or why not? What do you know about the graph?
Yes. 2(x-2)2 = 2(x-2)(x-2). There is only one x-intercept, and it is also the vertex.
400
Find a quadratic function given the parabola passes through (1, 5), (-2, 29), and (2, 9).
f(x) = 3x^2-5x+7