Find The Vertex
Find The X-intercepts
Find the Y-intercepts
Properties of Quadratics
Mixed Set
100
What is the vertex for the function:
f(x) = x2 + 6x + 6
Vertex: (-3, -3)
100
What are the x-intercepts of the quadratic function shown in the graph?
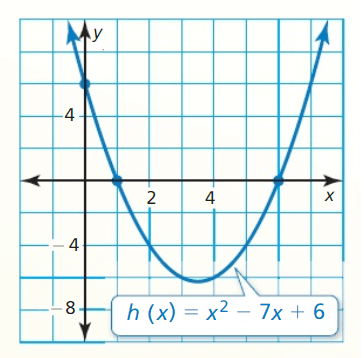
x = 1 and x = 6
{1, 6}
100
What is they y-intercept of the equation:
f(x) = x2
y-intercept: 0
(0, 0)
100
What is the standard form of a quadratic equation equation?
Ax2 + Bx + C = 0
100
What determines whether a function will have a maximum turning point or a minimum turning point?
Whether the highest power term is negative or positive.
200
The vertex for this quadratic function:
f(x) = x2 - 8x - 3
Vertex: (4, -19)
200
What are the solutions to the equation:
f(x) = x2 - 4
x = -2 and x = 2
{-2, 2}
200
Find the y-intercept of the equation:
f(x) = -x2 -6x -10
Y-intercept: -10
(0, -10)
200
What is the name of the line that divides a quadratic function exactly in half?
The Axis of Symmetry
200
Is the vertex of the quadratic function
f(x) = 5x2 + 10x - 2
a minimum or maximum point?
Minimum
300
Find the vertex for the quadratic function:
f(x) = x2 + 10x + 6
Vertex: (-5, -19)
300
The solutions of the equation
f(x) = x2 - 49 are:
x = 7 and x = -7
{7, -7}
300
What is the y-intercept for this quadratic function:
f(x) = x2 - 8x - 3
y-intercept: -3
(0,-3)
300
What is the name of the point on a quadratic function that will be the maximum or minimum of the function?
The vertex
300
What is the general formula for the vertex form of a quadratic function?
f(x) = a(x - h)2 + k
400
The coordinates of the vertex for this quadratic function:
f(x) = x2 - 4x + 8
Vertex: (2, 4)
400
What are the zeros of the equation
f(x) = x2 + 11x + 24 ?
x = -8 and x = -3
{-8, -3}
400
Find the coordinates of the y-intercept for the quadratic function:
f(x) = 3x2 + 2x - 1
y-intercept: -1
(0,-1)
400
How many solutions can a quadratic function have? List all possibilities.
1 solution, 2 solutions , or no solution
400
The factored form of the quadratic equation:
f(x) = x2 - 6x + 5
f(x) = (x - 5) (x - 1)
500
Use the formula -b/2a to find the axis of symmetry, then find the vertex of the following:
f(x) = x2 + 4x + 3
Axis of Symmetry: x = -2
Vertex: (-2,-1)
500
Find the zeros (x-intercepts) of the following:
f(x) = x2 - 8x - 20
x = 10 and x = -2
{-2, 10}
500
What is the y-intercept of the following equation:
f(x) = -2x2 + 5x -7
y-intercept: -7
(0,-7)
500
When a parabola opens upward, is it positive or negative and is it maximum or minimum?
Positive and Minimum
500
Find the y-intercept and vertex for this quadratic function.
14x = x2 + 49
y-intercept: (0, 49)
Vertex: (7, 0)