X intercepts
Transformations
Characteristics
Graphing
Writing Equations
100
Find the solutions to the equation: 3x2-7x+2
Answer: What is x=6, x=1
Steps:
1) Multiply a by c to get 6.
2) Find what adds to get -7x that multiplies to get 6
3) The factors (x-6) and (x-1) accomplish that and when you solve you get 6 and 1.
100
State all the transformations of the equation: -4(x+4)2-3
What is a reflection over the x axis, vertical stretch by 4, left 4 units, and down 3 units.
Steps:
1) Use a(x-h)2+k
2) A represents your stretch/compression factor. h represents your horizontal translation (inside lies), and k represents your vertical translation.
100
Identify the key characteristics of the graph (vertex, x intercepts, and y intercept(s)):
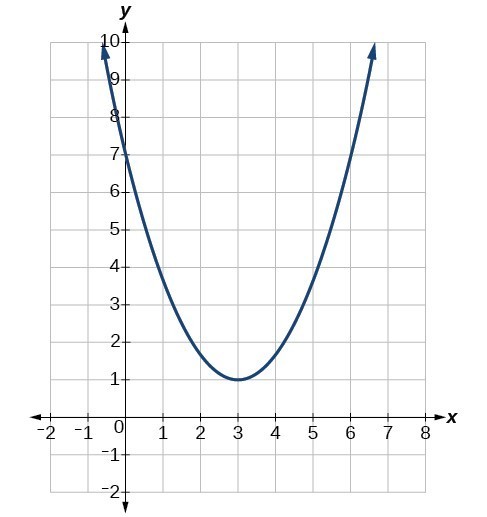
What are vertex: (3,1), y-intercept: (0,7), x intercept: N/A
Steps:
1) The vertex is the highest/lowest dip point on a graph (3,1)
2) The y intercept is where the graph crosses the y axis (0,7).
3) The x intercept is where the graph crosses the x axis, but there isn't one for the following graph.
100
Graph the following equation: -(x-7)2+1
What is a graph of:
Steps:
1) Find the vertex and plot it. Since it's a reflection across the axis, you draw the graph opening down.
100
Write an equation with a vertex of (2,1) and a reflection across the x axis.
What is an equation of: -(x-2)2+1
Steps:
1) Use vertex rules to write the vertex in the equation (inside lies)
2) Since it's a reflection, there would be a negative in front of the parenthesis.
200
Find the x intercepts to the equation: x2=12x-20
What is x=10, x=2
Steps:
1) Subtract 12x and 20 to to make the equation equal 0 (x2-12x+20=0).
2) Find what adds to get -12x and multiplies to get 20.
3) The factors (x-10), (x-2) accomplish that and when you solve them you get 10 and 2.
200
State all the transformations for the equation: 1/3(x-8)2+5
What is a vertical compression by 1/3, a translation right 8, and a translation up 5.
Steps:
1) Use a(x-h)2+k
2) A represents your stretch/compression factor. h represents your horizontal translation (inside lies), and k represents your vertical translation.
200
Identify the interval of increase on the graph (in terms of x):
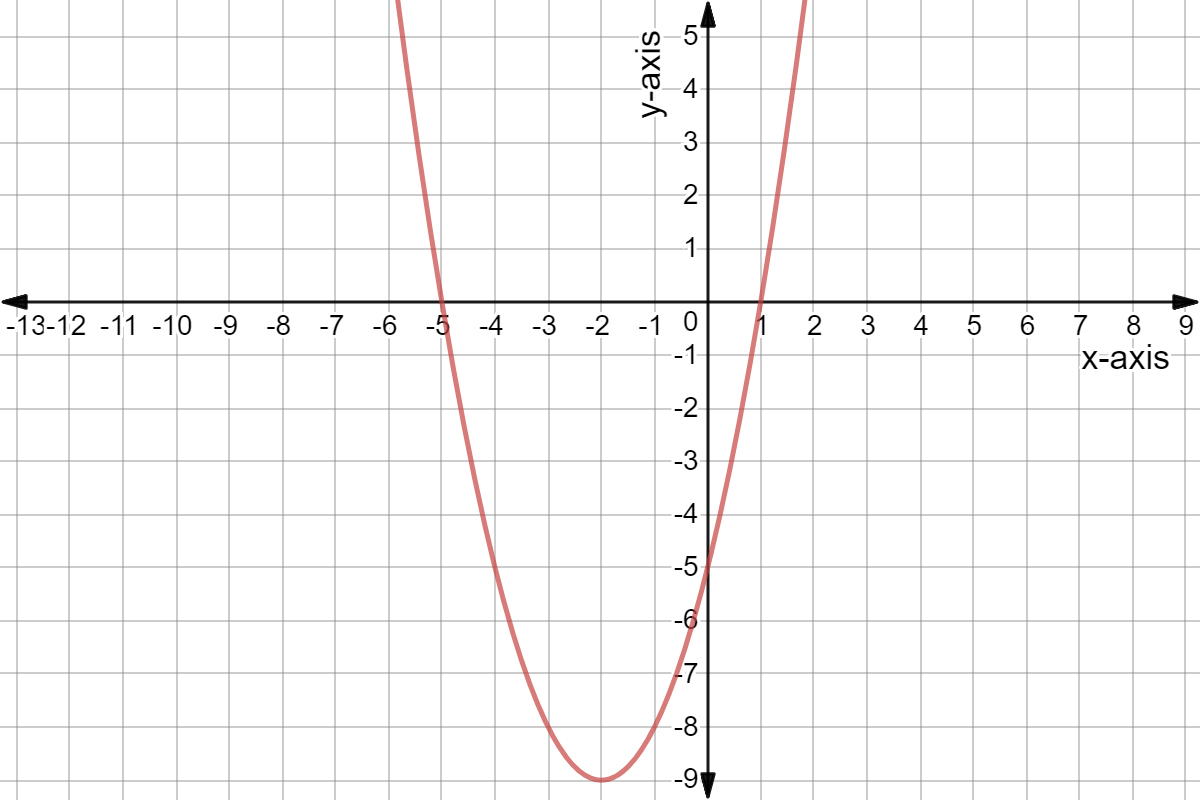
What is (-2, infinity), (-2 to infinity)
Steps:
1) The increased interval is where the graph is going up.
2) For this instance, it is from -2 to infinity.
200
Graph the following equation: 1/2(x+2)2-3
What is a graph of:
Steps:
1) Find the vertex and plot it.
2) Plug x values into the equation to plot other points since their is a compression of 1/2 to complete the graph.
200
Write a quadratic equation with the points (2,-12), (-1,-15), (-4,-90).
What is an equation -4x2+5x-6
Steps:
1) Use quadratic regression to find the equation.
2) Do Stat -> Edit and type in the x and y values.
3) Then do Stat -> Calc -> 5 to find the equation.
300
State 3 other names for x intercepts.
What are zeroes, solutions, and roots.
300
Write the equation with the following transformations:
Up 5, left 1, and a reflection across the x-axis.
What is -(x+1)2+5
Steps:
1) Use a(x-h)2+k
2) A represents your stretch/compression factor. h represents your horizontal translation (inside lies), and k represents your vertical translation.
300
State the positive and negative intervals on the graph.
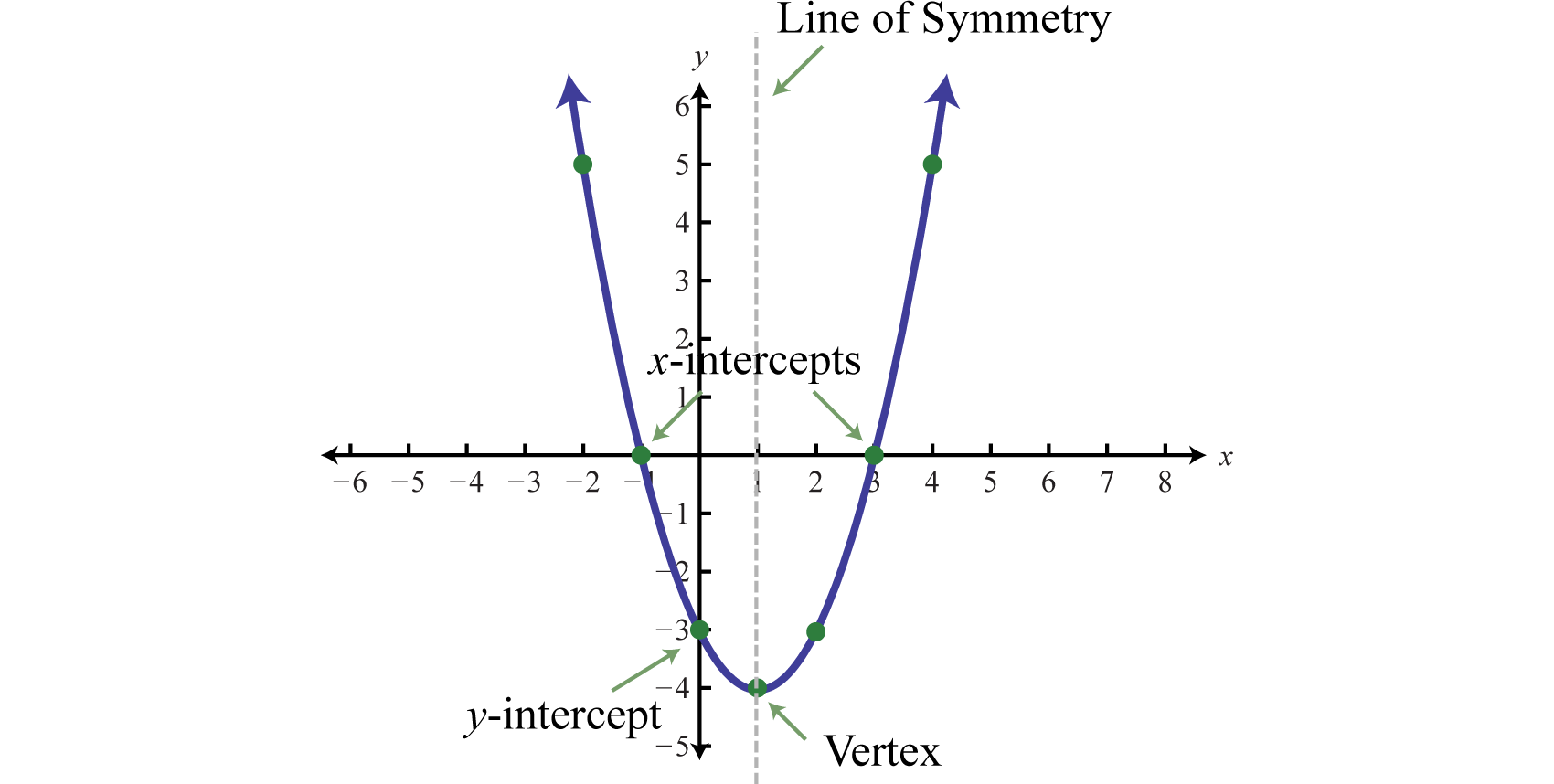
What is: negative: (-1,3), positive: (-infinity,-1),(3, infinity)
Steps:
1) For positive, it's where the graph goes over the 0 vertically, but you write it in terms of x
2) For negative, it's where the graph goes under the 0 vertically, but you write it in terms of x
300
Draw a graph with a vertex of (1,-2) and a y intercept of (0,-1)
What is a graph of:
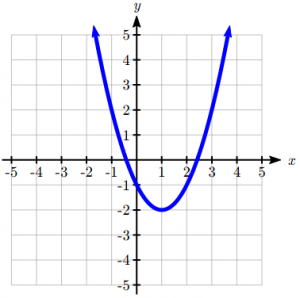
Steps:
1) First, plot the vertex ( over 1, down 2)
2) Then plot the y intercept and complete the graph.
300
Write an equation in vertex form with a vertex of (3,4) and a point at (1,3)
What is an equation of: -1/16(x-3)2+4
Steps:
1) First write the equation with the vertex in it.
2) Since an additional point is provided, you have to solve for a.
3) Put the x and y value of the additional point into your equation and solve for a.
4) Once solved, the a is -1/16.
400
Using this graph, state the x intercepts.
What are the factors?.png%3Frevision%3D1&usqp=CAU)
What are (-4,0) and (2,0). The factors are (x+4) and (x-2).
Steps:
1) To find the x intercepts on the graph, you see where the line crosses the x-axis.
2) The factors are the x intercepts set to zero.
400
What is the transformation done to the graph:
What is a translation down 8 units
Steps:
1) As you can see, on the graph, the original function f(x) is translation down 8 units.
400
Solve for the vertex of the equation: 4x2-16x+3
What is: (2, -13)
Steps:
1) Use the formula -b over 2a to solve for the x value of the vertex
2) Plug the values into the formula (16/2(4)) to get 2
3) Plug 2 into the original equation to get the y value of -13 and complete the vertex.
400
Describe how you would graph the following equation: 1.5x2+9x-6
What is: You would plot the vertex at (-3, -19.5) and the y intercept at (0,-6)
Steps:
1) Solve for the vertex using -b/2a and plug the x value into the original equation to get the y value.
2) Plot the y intercept since it's given.
400
Write a quadratic equation with the factors (x+3)(x-7)
What is x2-4x-21
Steps:
1)
500
Find the x intercepts of the equation: 6x2+x-15
What are x=3/2, -5/3
Steps:
1) Solve using the Quadratic Formula, identify the a, b, and c (a=6, b=1, c=-15)
2) Set up your quadratic equation ---
-(1) +- (√(1)^2-4(6)(-15))/ 2(6)
3) Solve the equation and get 3/2 and -5/3.
500
What is the following transformation done to the graph (Blue to red):
What is a vertical stretch
Steps:
1) As you can see, the blue graph to red graph got skinnier.
2) A vertical stretch occurs when the graph gets skinnier
500
State the domain and range of the graph:
What is a domain of (-infinity, infinity) and a range of (-infinity, 4]
Steps:
1) The domain is all of the x values from least to greatest.
2) The range is all of the y values from least to greatest.
500
Is a quadratic graph a one-to-one function. Explain.
What is: No because it does not pass both the vertical and horizontal line test.
Steps:
1) See if a line can be drawn through the graph both horizontally and vertically.
2) Since a quadratic does not pass the horizontal line test, it is not one to one.
500
The following coordinate points represents the average maximum and minimum temperatures recorded each month in North Carolina over a six month period. Write a quadratic equation that represents the data.
Points: (72.3, 46.5), (79, 55.3), (85.2, 62.6), (88.2, 67.1), (87.1, 68), (81.6, 60.4)
What is an equation of: -0.007x2+2.448x-94.523
Steps:
1) You type each corresponding x and y value into a table using stat -> edit.
2) Then, you click calculate after clicking quadratic regression.
3) You get your equation by plugging the a, b, and c values into a quadratic equation.