Simplify
Complex Operations
Discriminant
Solving Quadratics
Quadratic Graphs
100
What
i2
-1
100
Simplify the following:
(5i-7)+(4i+6)
-1+9i
100
When the discriminant is a positive number how many real solutions are there?
2
100
Solve the following Quadratic by Factoring:
x^2+4x+4=0
(x+2)(x+2)=0
x=-2
100
Based on a graph of a quadratic, what are the solutions (what characteristic)?
x-intercept(s)
200
Simplify:
sqrt(20)
2sqrt(5)
200
Simplify the following:
(3-5i)-(4-7i)
-1+2i
200
When the discriminant is zero, how many non-real solutions are there?
None.
There is 1 Real Solution.
200
Solve the following quadratic by factoring:
x^2-8x+7=0
(x-7)(x-1)=0
x=7,1
200
What are the solutions given the graph?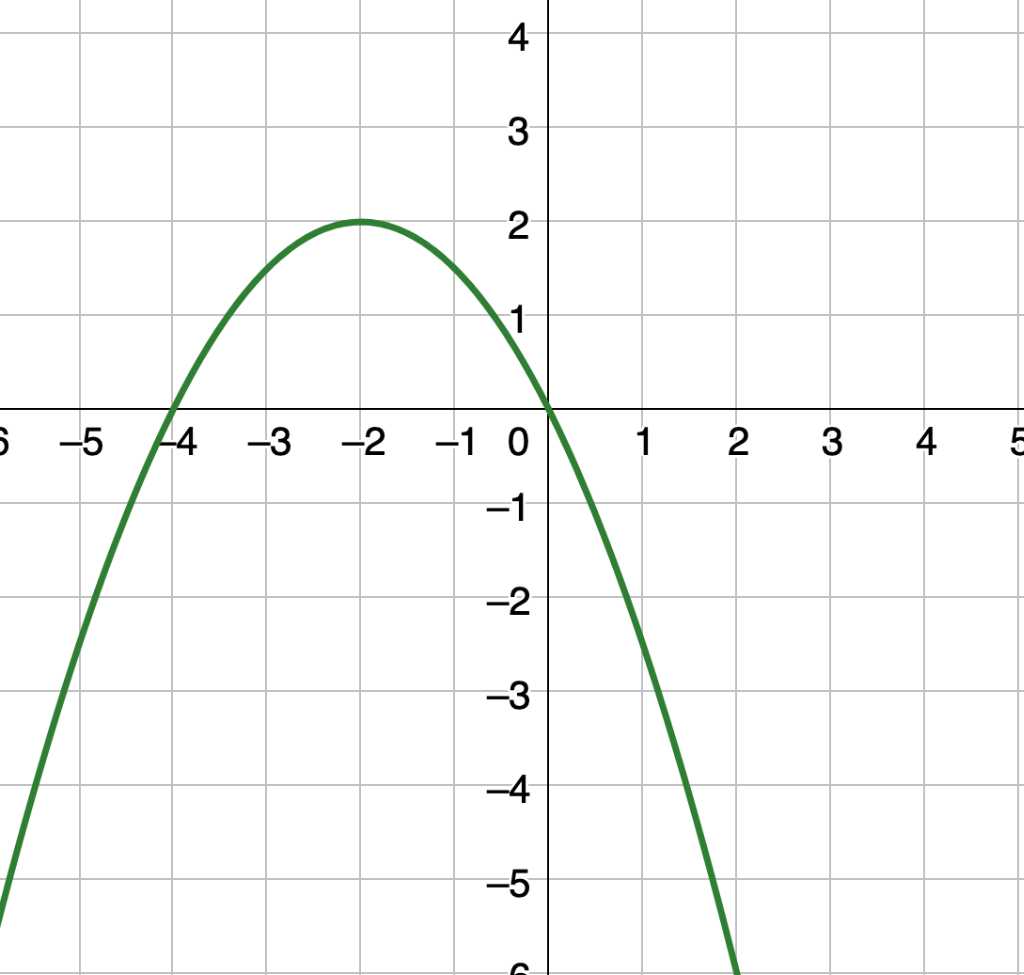 
x=-4, 0
300
Simplify:
i^45
i
300
Simplify the following:
(1+sqrt(-4))+(4-sqrt(-9))
5-i
300
Find the Discriminant of the following:
x^2-3x+5
(-3)^2-4(1)(5)
-11
300
Solve the following quadratic by taking the square root:
(x-4)^2=-25
x-4=+-5i
x=+-5i+4
x=5i+4, -5i+4
300
How many REAL solutions does the graph have?
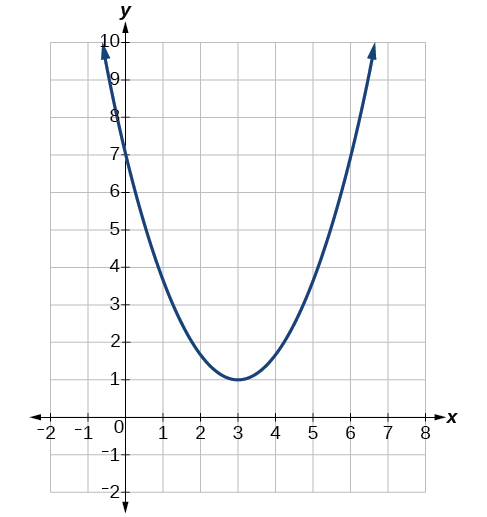
NONE Real!
(2 Non-Real)
400
Simplify:
sqrt(-45)
3isqrt(5
400
Simplify the following:
(3+6i)-(5-sqrt(-25))
-2+11i
400
Find the discriminant of the following:
x^2-4x-10
(-4)^2-4(1)(-10)
56
400
Solve the following quadratic:
2(x+1)^2-2=16
2(x+1)^2=18
(x+1)^2=9
x+1=+-3
x=+3-1=2
x=-3-1=-4
400
How many REAL solutions does the graph have?
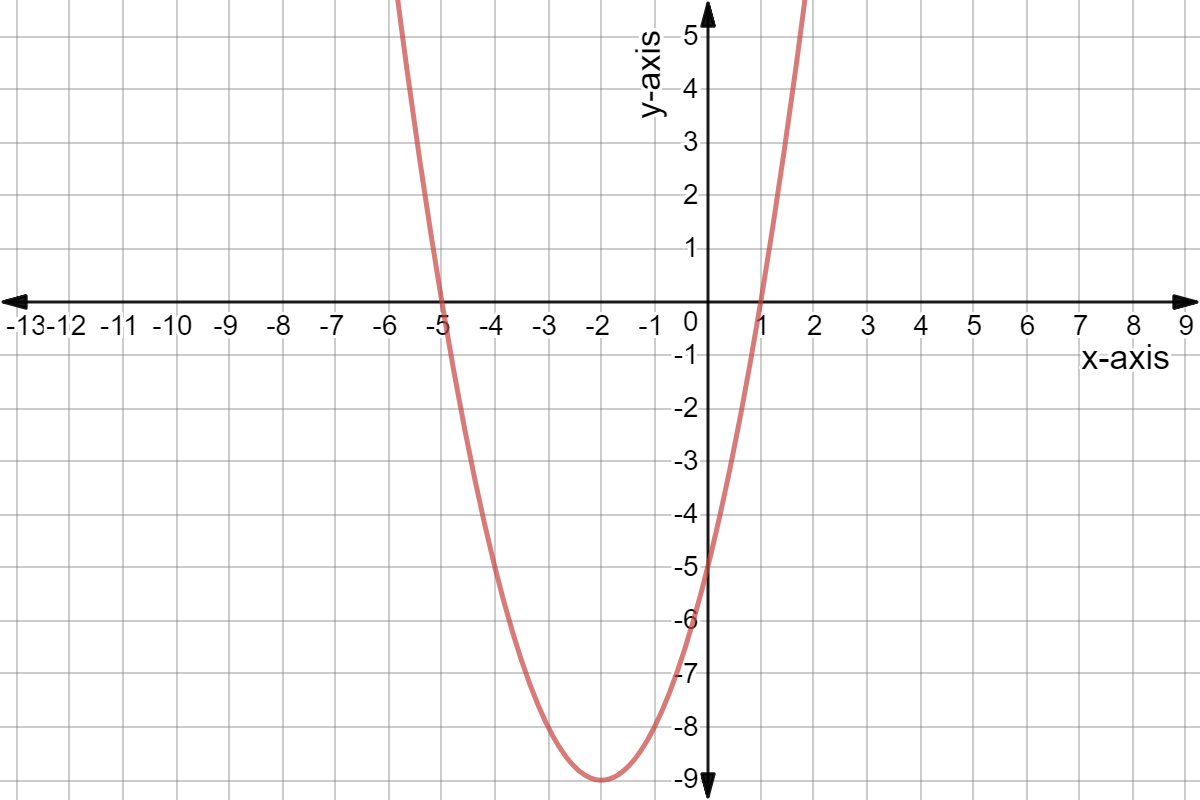
2 Real Solutions
500
Simplify:
-sqrt(-18)
-3isqrt(2)
500
Simplify the following:
(i^8-5)-(sqrt(-9)+i^3-3)
-1-2i
500
Find and evaluate the discriminant:
x^2+5x+4
(5)^2-4(1)(4)
9
2 Real Solutions
500
Solve the following Quadratic:
(x+3)^2+1=-15
(x+3)^2+1=-15
(x+3)^2=-16
x+3=+-4i
x=-3+-4i
x=-3+4i
x=-3-4i
500
How many REAL solutions does the graph have? What is the solutions?
There is 1 Real Solution!
x=0