Factor and Solve
Quadratic Formula
Vertex Form
Graphs of Quadratics
Complex Numbers
100
Factor the following quadratics completely:
x2+7x-8
(x+8)(x-1)
100
Solve using the quadratic formula
x^2-5x-14=0
7 and -2
100
What is the vertex of y = (x+5)² - 1
(-5,-1)
100
What are the x intercepts of y = -(x+1)(x-4)
(-1,0) (4,0)
100
Simplify the expression.
(4 + 2i) + (3 + 5i)
7 + 7i
200
Factor the following quadratics completely:
x2-9x=-14
(x-7)(x-2)
200
Solve the following quadratic using the quadratic formula:
3x2-4x-1=0
x=(2+-sqrt2)/3
200
What is the vertex of y = (x-7)(x-1)
(4,-9)
200
What is the vertex of y = -2(x-4)(x+6)
(-1,50)
200
Simplify the expression.
(8 + 2i) - (4 - 3i)
4 + 5i
300
Factor the following quadratics completely:
2x2+3x-20
(2x-5)(x+4)
300
Solve the following quadratic using the quadratic formula:
7x2-9=4x
x=(2+-sqrt67)/7
300
What is the vertex of y = -4(x-3)²
(3,0)
300
Does the graph of this equation open up or down? y = -4(x-2)² + 2
Open Down
300
What is the complex conjugate of
-6-18i
-6+18i
400
Factor the following quadratics completely:
5x2-9x+4
(5x-4)(x-1)
400
Solve using the quadratic formula
2x^2+3x-20=0
5/2 and -4
400
Write the following quadratic function in standard form. y = 3(x-3)² - 12
3x² - 18x + 15
400
What is the axis of symmetry and vertex of this parabola?
hint: written as x=__ and (__,__)
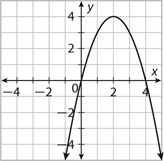
x=2, and (2,4)
400
What is the simplified form of
(9𝑖)−6(2𝑖−4)−8
16-3i
500
Solve the following equations by completing the square
x ^2 + 14x − 15 = 0
1 and -15
500
Solve using the quadratic formula
2x^ 2 − 7x − 13 = −10
(7+-\sqrt73)/4
500
Convert the following from standard to vertex form:
y=x2+6x+4
y=(x+3)2-5
500
What are the roots and y-intercept of the parabola below?
hint: written as three coordinate points
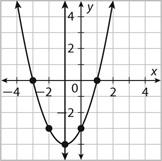
Roots: (-3,0), (1,0) and y-int: (0,-3)
500
14. What is the simplified form of
(5i^3)(2i^5)
10