Basic knowledge
Equations
Word problems
100
The quadratic function
What is f(x)=ax2+bx+c?
100
Solve the equation by factoring:
u2-5u-14=0
u2-5u-14=0
u2+2u-7u-14=0
u(u+2)-7(u+2)=0
(u+2)(u-7)=0
u+2=0 u−7=0
u=−2 OR u=7
u=-2 and u=7
100
If the sum of two numbers is equal to 17 and their product is equal to 60, what are the numbers?
x+y=17
xy=60
Now, we can rearrange equation 1 to get y=17−x. Substituting this expression into the second equation, we have:
x(17−x)=60
Expanding the parentheses and rearranging the equation, we have:
17x−x2=60
x2−17x+60=0
Now, we can factor the equation to solve:
x2−17x+60=0
(x−12)(x−5)=0
The numbers are 12 & 5
200
The "b" value in x2+5x+6
What is 5?
200
Factor the equation x2+4x-5
x2 + 4x – 5
x2-1x+5x-5
x(x-1)+5(x-1)
(x-1)(x+5)
200
The difference between the squares of two consecutive odd numbers is equal to 48. Find both numbers.
Representing the first number with x, we can deduce that a consecutive odd number is equal to x+2. Therefore, using the information in the statement, we form an equation with the squares of the consecutive numbers:
(x+2)2−x2=48
Expanding, simplifying and solving, we have:
x2+4x+4−x2=48
4x+4=48
4x=44
x=11
The consecutive odd numbers are 11 and 13.
300
The equation to find the vertex
What is - b/2a?
300
Factor the Equation
x2+15x=-50
x2+15x+50=0
x2+5x+10x+50=0
x(x+5)10(x+5)
(x+5)(x+10)
300
Rahul and Rohan have 45 marbles together. After losing 5 marbles each, the product of the number of marbles they both have now is 124. Find out how many marbles they started with
The number of marbles Rohan had = 45 – x.
The number of marbles left with Rahul after losing 5 marbles = x – 5
The number of marbles left with Rohan after losing 5 marbles = 45 – x – 5 = 40 – x
The product of number of marbles = 124
(x – 5) (40 – x) = 124
40x – x2 – 200 + 5x = 124
– x2 + 45x – 200 = 124
x2 – 45x + 324 = 0
This represents the quadratic equation. Then by solving the given equation for x, we get:
x = 36 and x = 9
So, the number of marbles Rahul had is 36 and Rohan had is 9 or vice versa.
400
The total values of "a", "b" , and "c" in 2x2-3x+4
What is 3
400
Solve the equation by factoring
y2=11y−28
y2−11y+28=0
y2-7y-4y+28=0
y(y-7)-4(y-7)=0
(y−4)(y−7)=0
y−4=0
y=4
OR
y−7=0
y=7
y=4 and y=7
400
If the area of a rectangle is 84 sq units and the longer side is 5 units more than the shorter side, then find the length of both sides. Let the shorter side be x.
The longer side's length will be x+5. The equation will be x(x+5)=84. We simplify that to x2+5x=84. Then, x2+5x-84. 2 numbers that equal 5 and multiply to -84 are 12 and -7.
x2+12x-7x-84=0 (x-7)(x+12)
The lengths are 7 and 12
500
The formula for x in the equation ax2+bx+c=0
What is x = [-b ± √(b2 - 4ac)]/2a?
500
Solve by Factoring
z2-16z+61=2z-20
z2-16z+61=2z-20
z2-18z+81=0
(z-9)2=0
z=9
500
The figure below has an area of 100 square units. Find the value of x
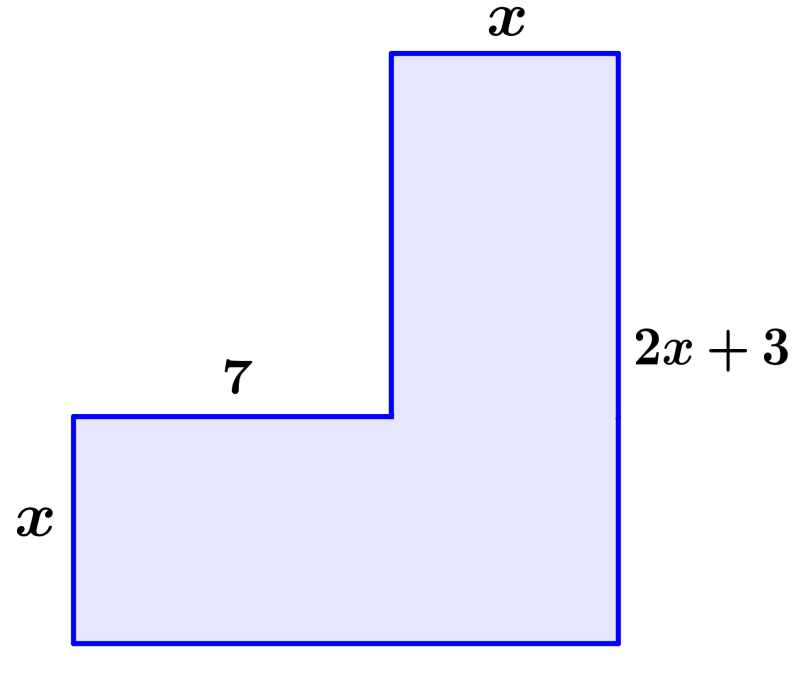
We can divide the figure into two rectangles, one rectangle has the area of 7x and the other rectangle has the area of x(2x+3). Adding these areas, we have:
7x+x(2x+3)=100
Expanding and simplifying, we have:
7x+2x2+3x=100
2x2+10x−100=0
Now, we can divide the entire equation by 2 and solve by factoring:
x2+5x−50=0
(x+10)(x−5)=0
x=−10 or x=5
Since we can’t have a negative length, the answer is x=5.