Domain and Range
Function Notation
Equivalent Functions
Symmetric Points
Other Attributes
100
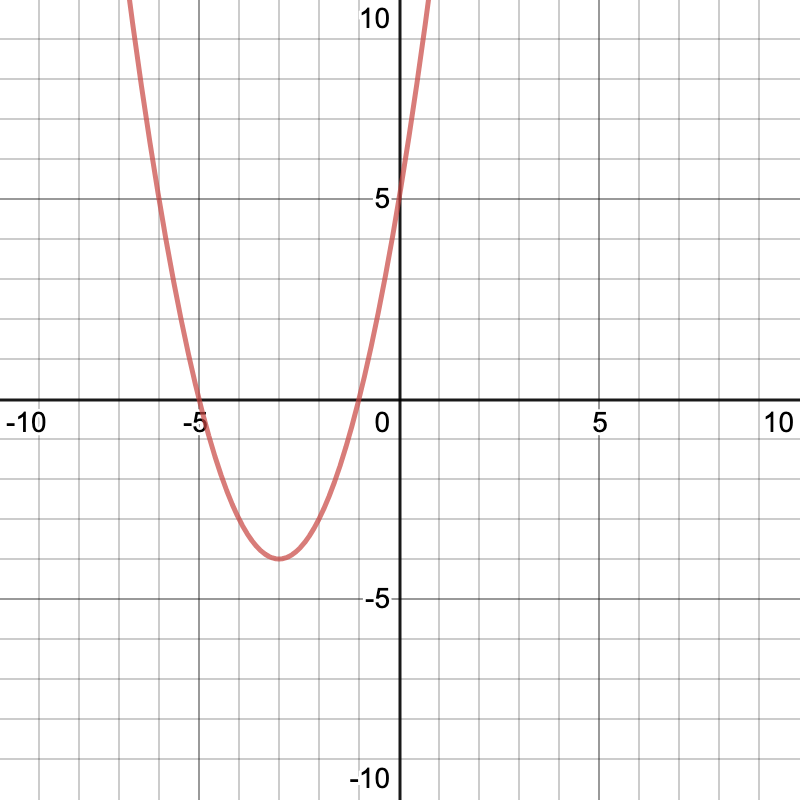
What is the range of this function?
y > -4
y >= -4
y < -4
y <= -4
B)
y >= -4
100
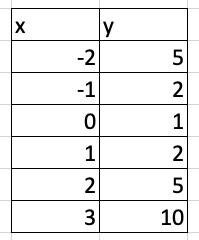
Find f(2) on the table.
y=5
100
Find the equation that is equivalent to this function:
y=x^2+2x-6
Choices:
y=(x+1)^2+7
y=(x+1)^2-7
y=(x-1)^2+7
y=(x-1)^2-7
B)
y=(x+1)^2-7
100
Use the equation
y=x^2+1
and find the symmetric point to (2, 5)
(-2, 5)
100
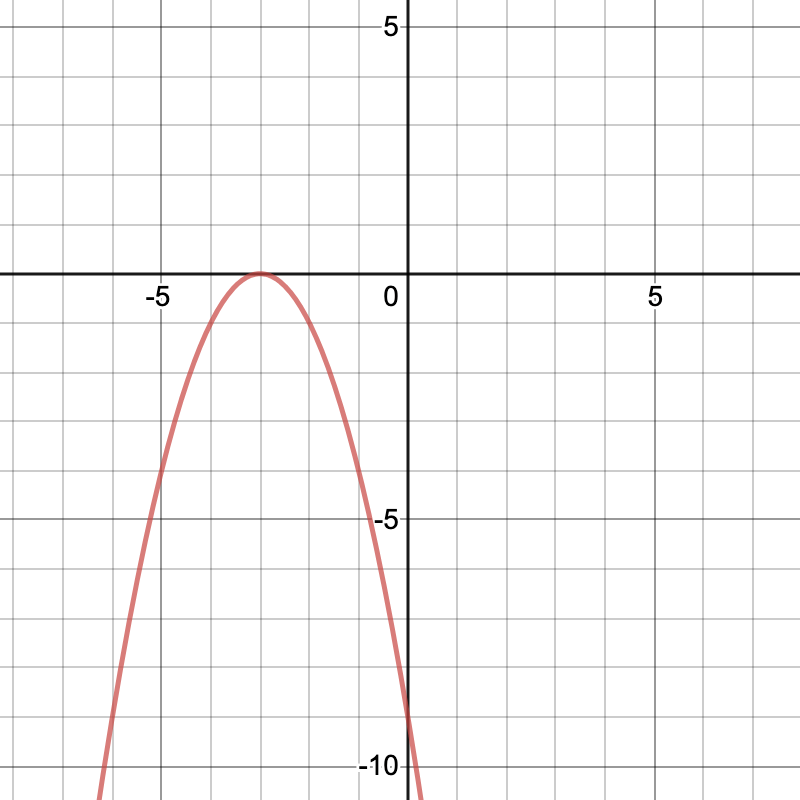
Find the y-intercept.
(0, -9)
200
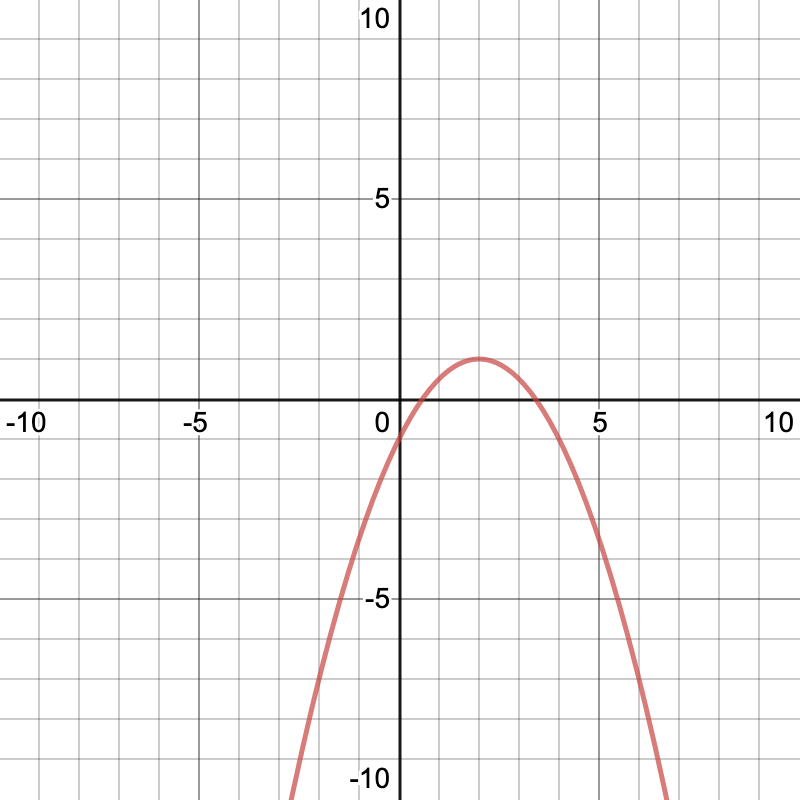
What is the range of this function?
D)
y <= 1
200
Find f(x)=-4 on the table.
x=-5 and x=-1
200
Find the function that is equivalent to this function:
y=x^2+4x+1
Choices:
y=(x+4)^2+1
y= (x+1)^2+4
y=x^2+4x+3
y=(x+2)^2+3
D:
y=(x+2)^2+3
200
Use the equation
y=(x+1)^2-3
and find the symmetric point to (1, 1)
(-3, 1)
200
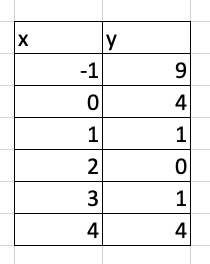
Find the y-intercept on the table.
(0, 4)
300
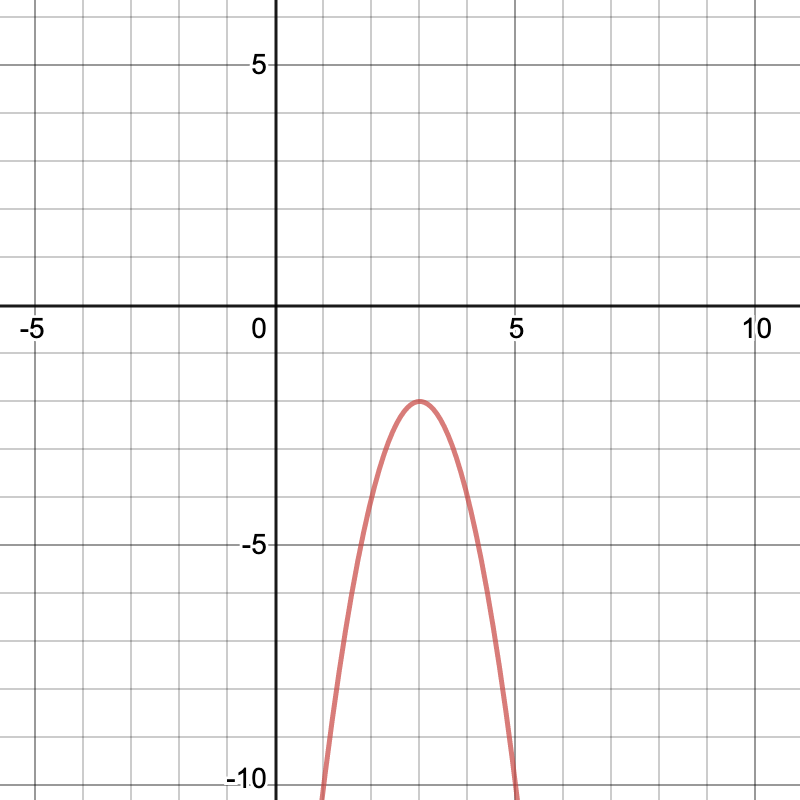
What is the domain of the graph?
ALL REAL NUMBERS!
300
For the function:
f(x)=5(x+3)^2-4
find:
f(-4)
y=1
300
Find the function that matches:
y=1.5(x+2)^2+3
Choices:
y=-x^2-4x+1
y=x^2+4x+7
y=x^2+6x+9
y=1.5x^2+6x+9
D) y=1.5x^2+6x+9
300
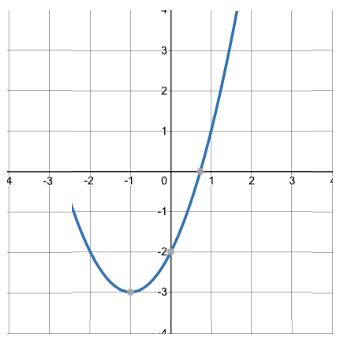
Find the symmetric point to (1,1).
(-3, 1)
300
Find the vertex of this function:
y=x^2+4x+1
(-2, -3)
400
Write the correct domain for this graph.
0 <= x <= 3.5
400
Use this equation:
f(x)=x^2+4x+1
to find:
f(x)=-3
x= -2
400
Find the function that matches:
y=-1/2(x-4)^2+7
Choices:
y=-1/2x^2+4x+7
y=-1/2x^2+4x-7
y=-1/2x^2+4x-1
C)
y=-1/2x^2+4x-1
400
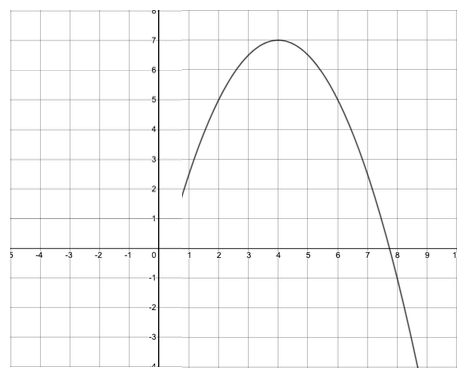
Find the symmetrical point to (8, -1)
(0, -1)
400
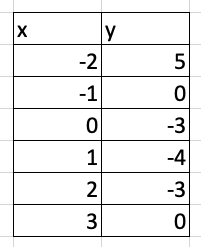
Find the zeroes on the table.
(-1, 0) and (3, 0)
500
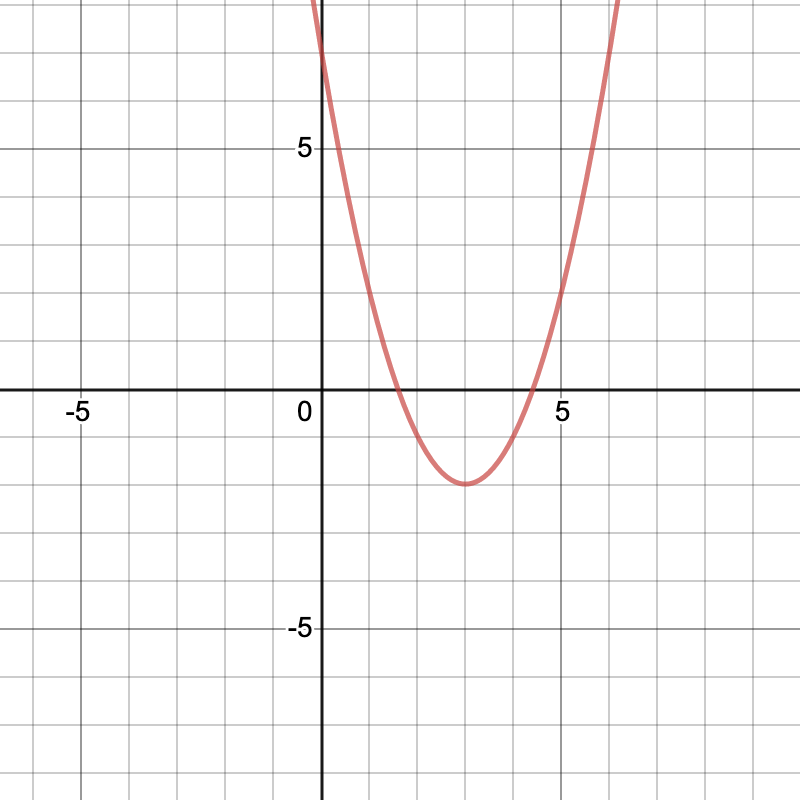
Write the range for this graph.
y >= -2
500
Use this equation:
y=(x-3)^2-2
to find:
f(x)=2
x=-1 and x=5
500
Write a function that opens upwards and has a vertex at (-2, 3).
HINT: VERTEX FORM
y=(x+2)^2+3
500
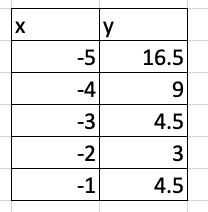
Find the symmetric point to (-4, 9)
(0, 9)
500
Find the zeroes on this equation.
y=(x+1)^2-9
(-4, 0) and (2, 0)