Umm, I Have Standards...
Taken to the Max! (or Min!)
We've Reached the Turning Point...
No Problems, Only Solutions (zeroes)
Oh, Word!
(problems)
(problems)
100
Rewrite the expression in standard form:
-3x + 2x2 + 17
2x2 - 3x + 17
100
If my leading coefficient is positive (a > 0), then the parabola faces _____________
Upward
100
What is the Vertex of the parabola below?
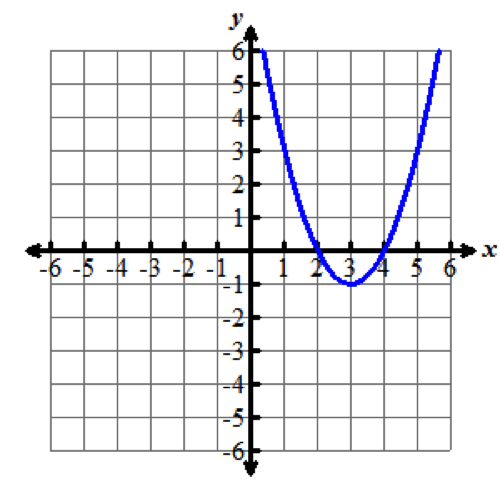
Vertex (Minimum):
(3, -1)
100
How many x-intercept(s) exist for the Quadratic Equation below:
1 x-intercept at the Origin (0,0)
(vertex "scrapes" x-axis)
100
The height of a diver is illustrated by the graph below:
How many seconds does it take for the diver to reach the surface of the pool?
It takes 3.5 seconds (x-intercept/zero/solution)
200
Rewrite the quadratic equation, in standard form:
5x2 - 12 = 4x
5x2 - 4x - 12 = 0
200
If my leading coefficient is negative (a < 0), then the parabola faces ___________________
Downward 
200
What is the equation of the Axis of Symmetry of the graph below?
Axis of Symmetry:
x = 3
200
What are the solutions to the quadratic equation below:
Solutions:
(-3 , 0) and (-5 , 0)
{-3 , -5}
200
A model rocket is launched from the roof of a building. Its flight path is modeled by
h(t) = -5t2 + 30t + 10
where h(t) is the height of the rocket above the ground in meters, and t is the time after the launch in seconds.
What is the initial height of the rocket when it was launched?
Initial Height (y-intercept):
10 meters
300
Rewrite the quadratic equation, in standard form:
4x - 5 = 6x2 + 3x - 1
6x2 - 1x + 4 = 0
300
If a parabola opens upward, then the parabola has a maximum / minimum (Choose One)
Minimum
300
Determine the Axis of Symmetry from the equation below:
x2 - 8x + 13 = 0
Axis of Symmetry:
x = 4
300
Find the zeroes of the following quadratic equation:
y = (x - 4)(x + 5)
Zeroes:
x = 4 and x = -5
300
A ball is thrown into the air from the edge of a 48-foot-high cliff so that it eventually lands on the ground. The graph below shows the height, y, of the ball from the ground after x seconds.
For which interval is the ball’s height always decreasing?
0 ≤ x ≤ 2.5
0 < x < 5.5
2.5 < x < 5.5
x ≥ 2
Choice 3: 2.5< x< 5.5
400
Rewrite in standard form & identify the coefficients:
8x + 4 = 10 + x2
a= ________ b = _________ c = _________
x2 - 8x + 6 = 0
a = 1 b = -8 c = 6
400
Does the quadratic equation below have a minimum or maximum value?
-2x2 + x - 1 = 0
Maximum
-2x2 + x - 1 = 0
Leading coefficient is negative; opens downward
400
Determine the Axis of Symmetry from the equation below:
y=(x - 4)2 - 2
Axis of Symmetry:
x = 4
400
How many solutions are there for the given quadratic equation below:
h(x) = 2(x - 4)2 +1
There are 0 solutions
(parabola DOES NOT cross x-axis)
400
A water balloon is catapulted into the air so that its height h(t), in feet, after t seconds is modeled by:
h(t) = -4.9t2 + 27t + 2.4
What was the height of the water balloon after 4 seconds?
Input t=4 OR Use Calculator - Table
Height = 32 feet
500
Rewrite in standard form & identify the coefficients:
4(x + 5)2 = 0
a = ________ b = _________ c = _________
4x2 + 40x + 100 = 0
a = 4 b = 40 c = 100
500
What is the maximum / minimum value of the quadratic equation below:
x2 + 4x - 12 = 0
Minimum Value
-16
500
Identify the Vertex & Axis of Symmetry, given the table below:
Vertex: (0 , -2)
Axis of Symmetry: x = 0
500
What are the zeroes of the following quadratic function?
Zeroes: (3 , 0) and (6 , 0)
500
a) 4 seconds (time is takes cross x-axis)
b) 2 seconds (Axis of Symmetry)
c) 64 feet (Maximum - Vertex)