Transformers
What's a Name by any other Name?
Everything you own in box!
Use the Formula Bro!
Its getting wordy?
Its Average.
100
Write the quadratic expression in standard form.
3x2+4x = -9
Standard Form:
3x2+4x+9=0
100
Consider the Graph.
What is the vertex?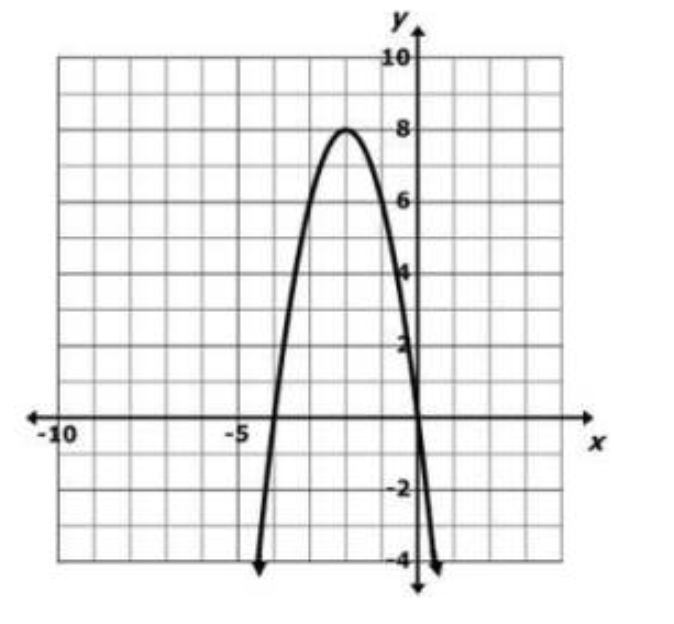 
(-2 , 8)
100
Factor the quadratic expression completely:
x2-4x+3
(x - 1)(x - 3)
100
Consider the function below:
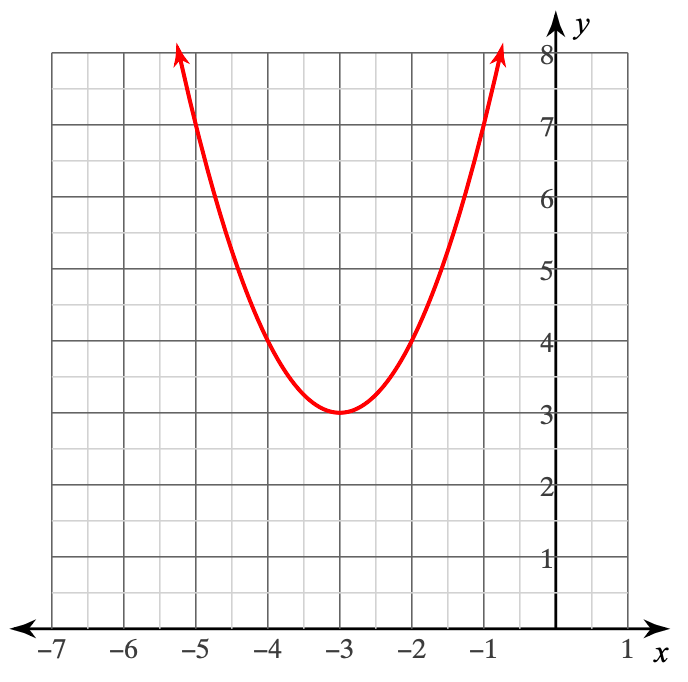What type of roots does the function have?
A. Rational
B. Irrational
C. Complex
Complex
100
Nathaniel kicks a football. The graph below shows the height of the football, h, in meters after, t, seconds. After how many seconds does the football hit the ground?
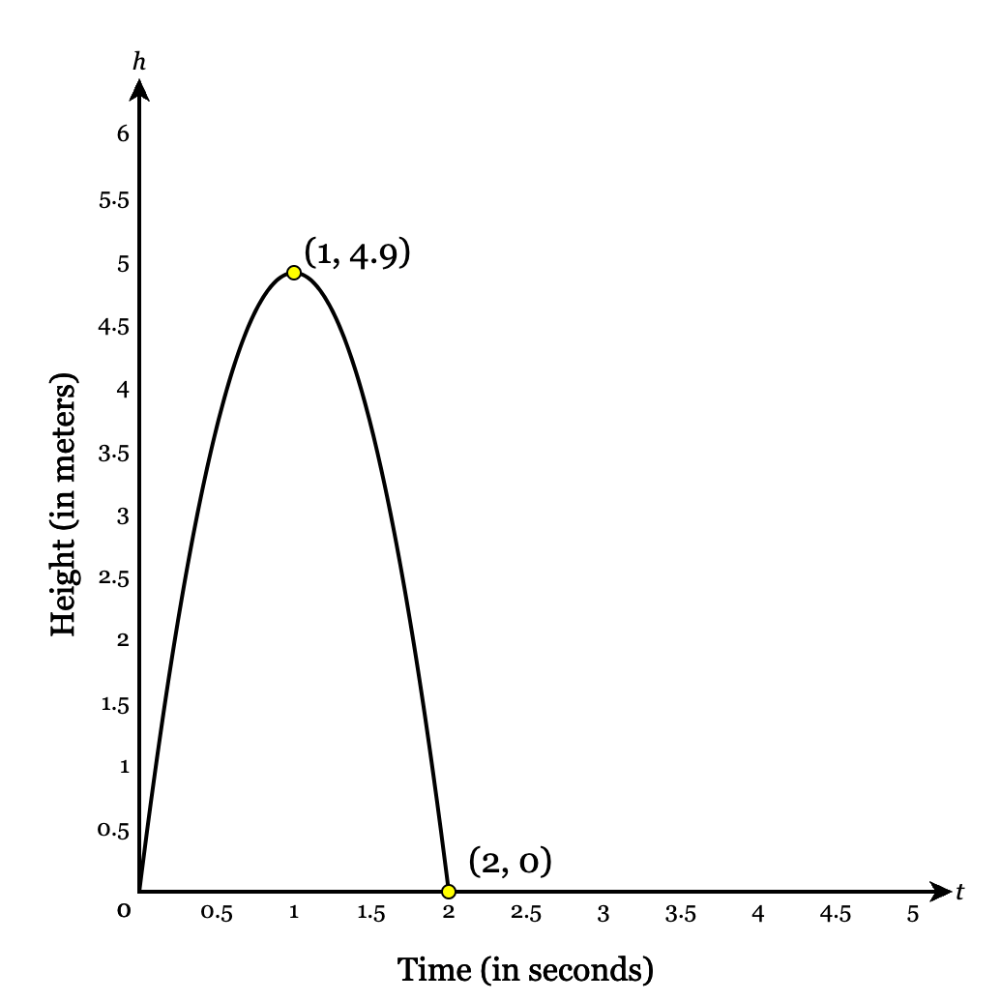
2 seconds
100
Given the function defined in the table below, find the average rate of change, in simplest form, of the function over the intervale
1 <=x<=3 
3
200
Write the quadratic expressions in standard form.
-2x2 = 5x - 12
Standard Form:
-2x2-5x+12=0
200
Consider the function below:
f(x) = 3x2 - 18x + 24
What is the line of symmetry of the function?
x = 3
200
Factor the quadratic expression completely:
-x2 + 6x - 8
-(x - 4)(x - 2)
200
Consider the function:
4x2 = 135 - 12x
Use the quadratic formula to determine the zeros of the function.
x = {9/2 ,-15/2}
200
Jacob launches a toy rocket from a platform. The graph below shows the path of the rocket including height, h, in feet and t, for seconds.
What was the maximum height that the rocket reached?
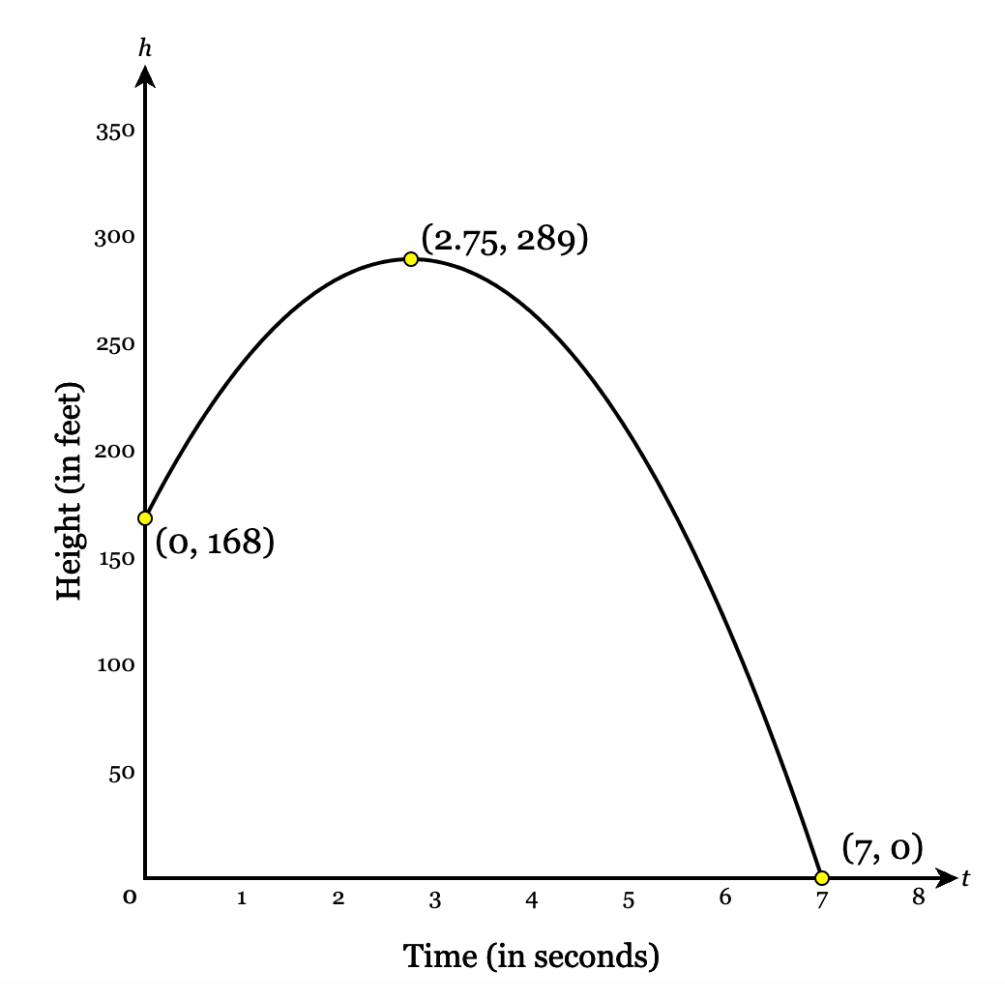
289 feet
200
Given the function defined in the table below, find the average rate of change, in simplest form, of the function over the interval
6 <= x <= 30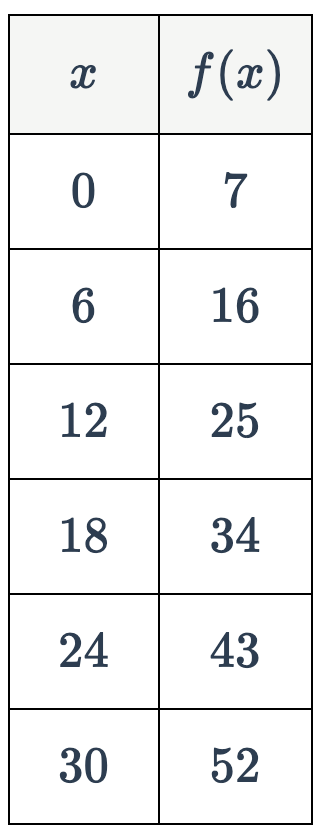
3/2
300
Write the linear equation in standard form.
y=1/2x-4
Standard form:
-x+2y=-8
300
Consider the function graphed below: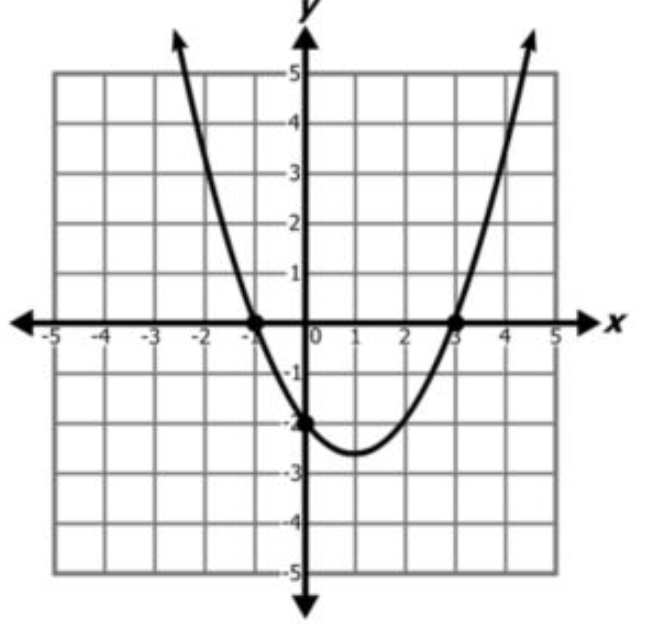 
What are the roots of the function?
(-2,0)
(3,0)
300
Factor the expression completely:
4x2 - 45x + 50
(x - 10)(4x - 5)
300
Consider the quadratic function below:
5x2 + 6x + 12 = 0
Using the quadratic formula, determine the solutions.
No Solution
300
Meena hits a softball into the air. The graph below shows the height of the softball, h, in feet after t seconds. What interval is the ball height decreasing?
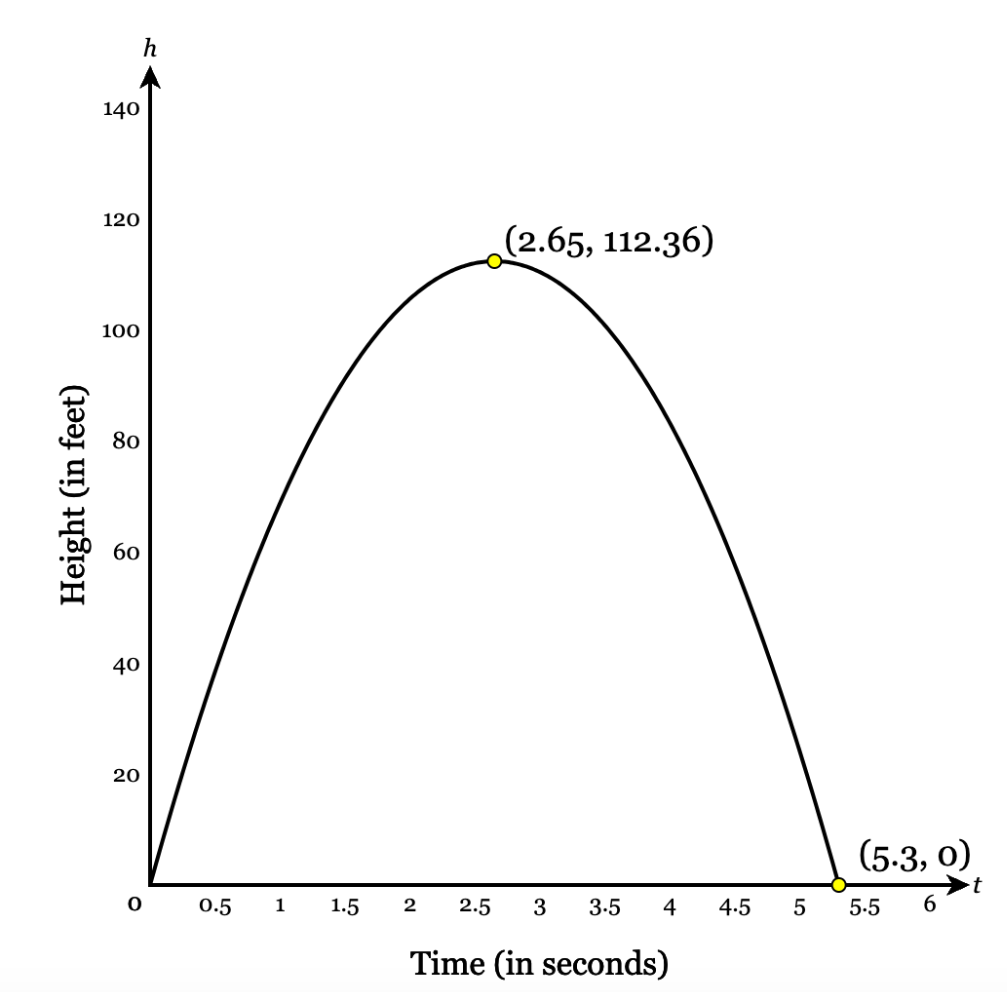
2.65 seconds < x < 5.3 seconds
300
Given the function
g(x) = x2 - 5x - 2
determine the average rate of change of the function over the interval
1 <= x <= 9
5
400
Which of the following linear and quadratic expression are in standard form?
Select 2 answers that apply.
[A] 3x2 + 9x = -10
[B] 2x + 9y = 12
[C] y = x - 2
[D] x2 - 8x + 12 = 0
[E] y = 2x + 3
Functions that are in standard form:
B & D
400
Consider the graphed function:
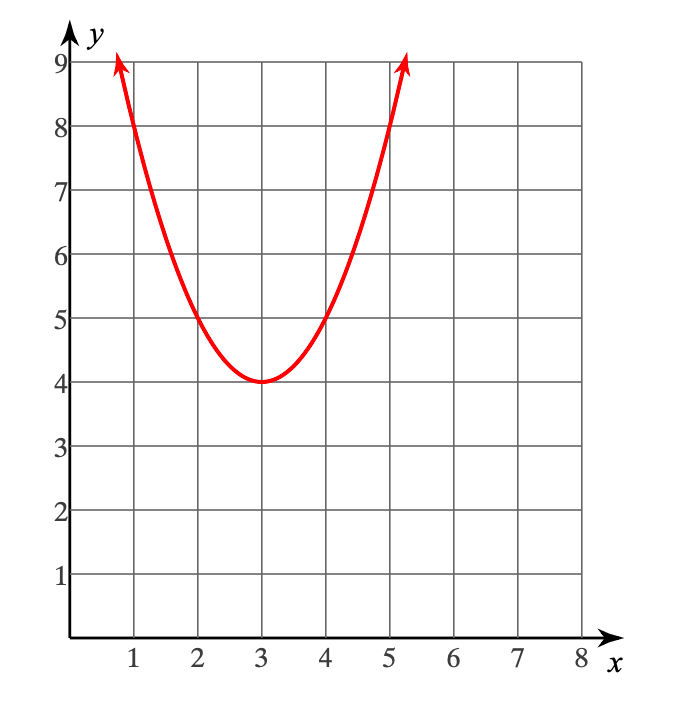
Write the graphed function in standard form?
y= x2 - 6x + 13
400
Factor the expression completely:
4x2=-3x2 - 54x + 81
(7x - 9)(x + 9)
400
Consider the quadratic function below:
2x2 - 12x = 6
Using the quadratic formula determine the x-intercepts.
x = {3 + sqrt12 , 3 - sqrt12}
x = {3 + 2sqrt3 , 3 - 2sqrt3}
400
A tennis ball is dropped from a certain height. Its height in feet is given by
h(t) = -16t2 + 196
"t" represents the time in seconds after the ball is dropped. How long is the ball in the air?
3.5 seconds
400
Given the function
h(x) = -x2 + 7x + 18
determine the average rate of change of the function over the interval
1 <= x <= 10
- 4
500
Consider the equation below.
Solve for r
c = pir^2
r = sqrt(c/pi
500
Consider the function below:
f(x) = -4(x + 5)2 - 10
What is the vertex of the function?
(-5 , -10)
500
DOUBLE JEOPARDY
What is the standard form for all quadratic expressions?
ax2 + bx + c =0
500
Consider the function below:
6x2 - 9x + 1 = 2
Using the quadratic function, determine the x - intercepts.
x = {(9+sqrt105)/12 , (9 - sqrt105)/12}
500
A toy rocket is launched from the platform. The height of the rocket in feet is given by
h(t) = -16t2 + 56t + 32
where "t" represents the time in seconds after launch. What is the rocket's initial height?
32 feet
500
Consider the graph of a function, which shows the number of customers in a department store, y after x hours of the store opening.
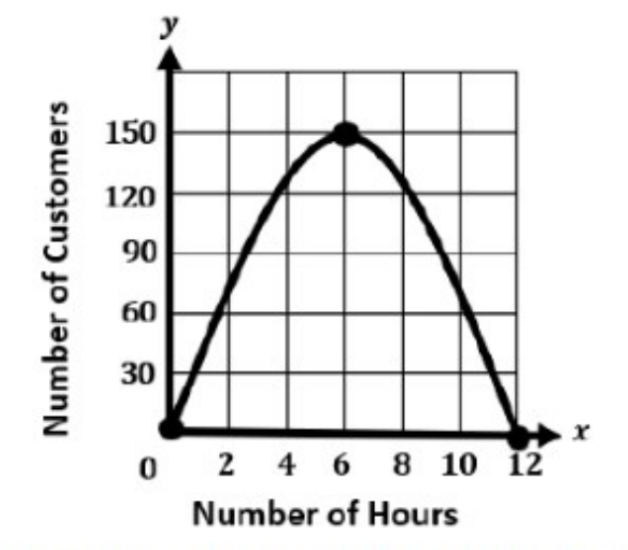
What is the approximate average rate of change between 6 hours and 12 hours?
-25 customers per hour
600
Write the quadratic below in standard form:
y = -3(x - 9)2 + 12
Standard Form:
y = -3x2 - 54x + 255
600
Consider the function
x2 + 14x - 98 = 0
Write the equation below with the blanks filled in with the correct numbers.
(x + _____ )2 = __________
(x + 7)2 = 147
600
Factor the expression completely.
9x2 + 43x + 100 = -44x - 20
3(3x + 5)(x + 8)
or
(9x + 15)(x + 8)
600
A toy rocket is launched from the platform. The height of the rocket in feet is given by
h(t) = -4x2+10x + 24
where "t" represents the time in seconds after launch. When will rocket reach a height of 28 feet?
0.5 seconds
2 seconds