Evaluate/Solve
Vertex Form
Factored Form
Standard Form
100
Evaluate f(-3)
f(x)=-(x+1)^2-5
-9
100
Find the vertex:
f(x) = -2(x-3)^2+8
(3,8)
100
Find the x-intercepts:
f(x)=-3(x-3)(x+1)
x=3
and
x=-1
100
What is standard form?
f(x)=ax^2+bx+c
200
Solve f(x)=0
f(x)=(x-2)^2-9
f(x) = 5
or
f(x) = -1
200
Find the y-intercept:
f(x) = -2(x-3)^2+8
(0,-10)
200
Find the y-intercept:
f(x)=-3(x-3)(x+1)
(0,9)
200
Go from factored form to standard form
f(x)=(x-3)(x+7)
f(x)=x^2+4x-21
300
Solve f(x) = 0 by going from standard form to factored form.
f(x)=x^2-2x-8
x = -2
x= 4
300
Find the x-intercepts:
f(x) = -2(x-3)^2+8
(1,0) and (5,0)
300
Find the AOS and Vertex:
f(x)=-3(x-3)(x+1)
AOS: x=1
f(1) = 12
Vertex = (1,12)
300
Go from standard form to factored form...
f(x)=(x-5)(x+2)
f(x)=x^2-3x-10
400
Solve f(x) = 0 by going from standard form to factored form.
f(x)=x^2-5x+6
x=3
x=2
400
Create an equation in vertex form for the graph...
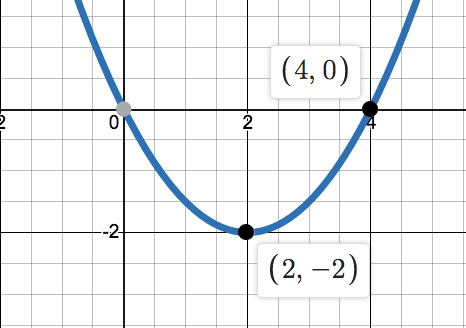
f(x)=1/2(x-2)^2-2
400
Create an equation in factored form for the graph...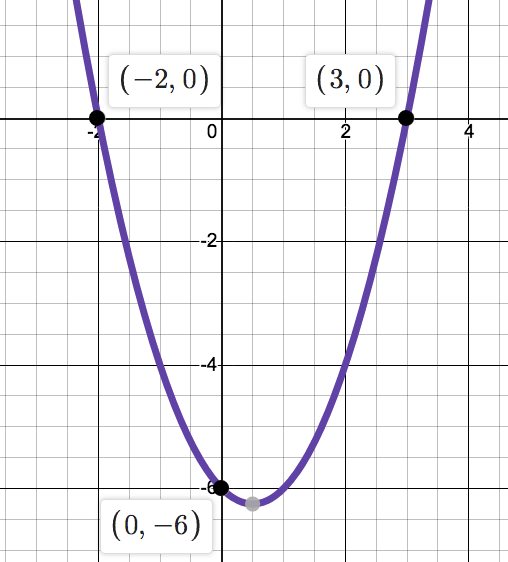
f(x)=(x-3)(x+2)
400
Go from standard form to factored form...
f(x)=2x^2+x-15
f(x)=(2x-5)(x+3)
500
Solve for 'a' when the vertex is (-1,-6)
f(x)=a(x-2)(x+4)
a = 2/3
500
Find the 'a' value of the equation given the graph. Then give the equation in vertex form.
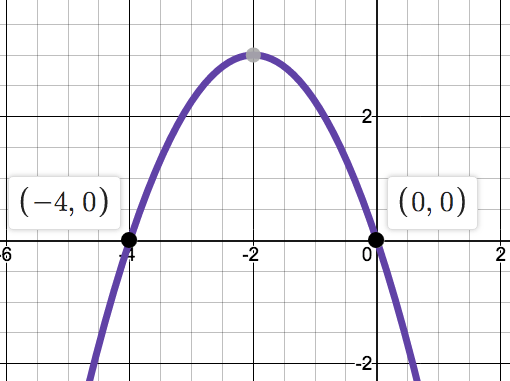
f(x)=-3/4(x+2)^2+3
500
Find the 'a' value of the equation given the graph. Then give the equation in factored form.
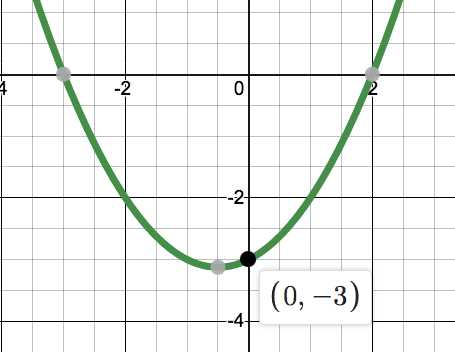
f(x)=1/2(x+3)(x-2)
500
Find the vertex...
f(x)=x^2+8x+15
Factored Form: f(x)=(x+3)(x+5)
Roots: x = -3 and x = -5
AOS: x = -4
f(-4) = -1
Vertex: (-4,-1)