Vertex
Quadratic Forms
Factoring
Solving
Wild Card
100
What is the Vertex of the graph.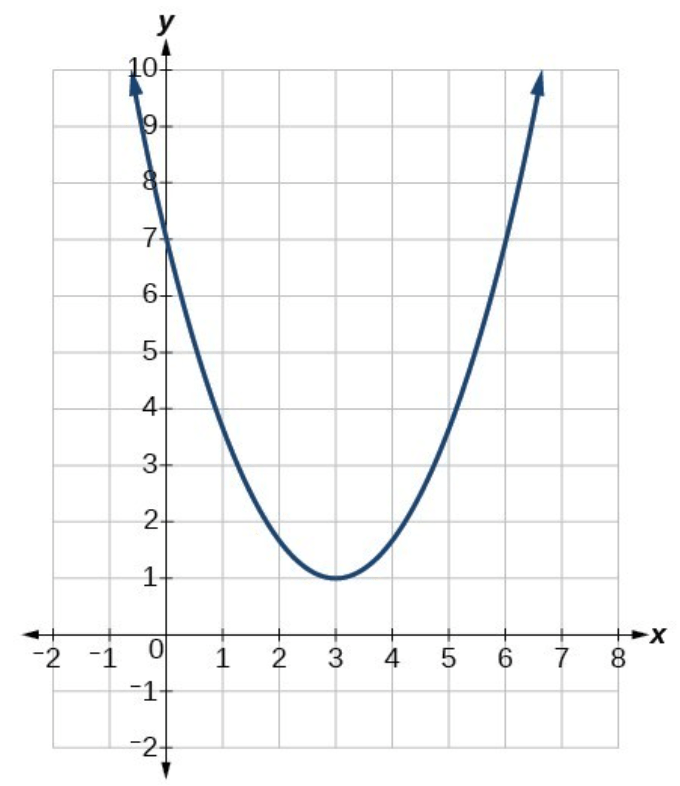 
Vertex = (3, 1)
100
Which form give you the y-intercept?
Standard From
ax2+bx + c
C = y-intercept
100
Factor the trinomial
x2+ 7x - 30
(x -3)(x + 10)
100
Solve for x
x2 - 36 = 0
x = -6
x = 6
100
Simplify the radical
√360
6√10
200
What is the vertex of f(x) = 4(x - 3)2 + 11
(3, 11)
200
Given factored form y = (x - 5)(2x + 3), what is the equation in standard form?
y = 2x2 - 7x - 15
200
Factor the Trinomial
4x2- 44x + 120
4(x - 5)(x - 6)
200
solve
(3x - 7)(2x + 8) = 0
x = 7/3
x = -4
200
What is the domain of all Quadratics?
(-∞, +∞) or ALL Real Numbers
300
Given the axis of symmetry is x = -3
What is the vertex of y = x2+ 6x - 10
(-3)2+ 6(-3) - 10 = 9 - 18 - 10 = -19
Vertex = (-3, -19)
300
A quadratic is translated 6 units to the right and reflect down from the parent graph y = x2. What is the equations of the quadratic in vertex form?
y = -(x - 6)2
300
-5x2 + 45x
-5x(x - 9)
or
5x(9 - x)
300
Solve
x2+ 18x + 81 = 0
x = -9
300
For what interval is the quadratic negative
f(x) = (x + 7)(x - 2)
-7 < x< 2
400
What is the Axis of symmetry of the quadratic
y = (x - 5)(x + 3)
AoS = +1
400
What is the quadratic written in Standard From?
y = (x + 3)2 + 7
y = x2 + 6x + 16
400
Factor the expression
x2- 81
(x - 9)(x + 9)
400
Solve for x.
2x2- 12x - 42 = 0
x = 3 + √30
x = 3 - √30
400
Simplify the expression
(4+ 7i) - 2(6 - 3i)
-8 + 13i
500
Knowing that the Vertex is at. (-4, 2)
What is the missing value of b in the equation
y = x2+ bx +10
AoS = b/-2a
b/-2(1) = -4
b = + 8
500
Write the quadratic in Vertex form.
y = x2 + 8x - 10
y = (x + 4)2 - 26
500
Factor the trinomial
6x2 - 23x+ 20
(2x - 5)(3x - 4)
500
Solve for x
6x2+ 6x +15 = 0
x = i
x = -2i
500
Simplify the expression
(4 + 2i)(3 - 3i)
18 - 6i