Domain & Range
Roots & AOS & Optimal Value
The cost to run a machine..
A ball is thrown...
Forms of a quadratic
Word problems
100
Is the following relation a function?
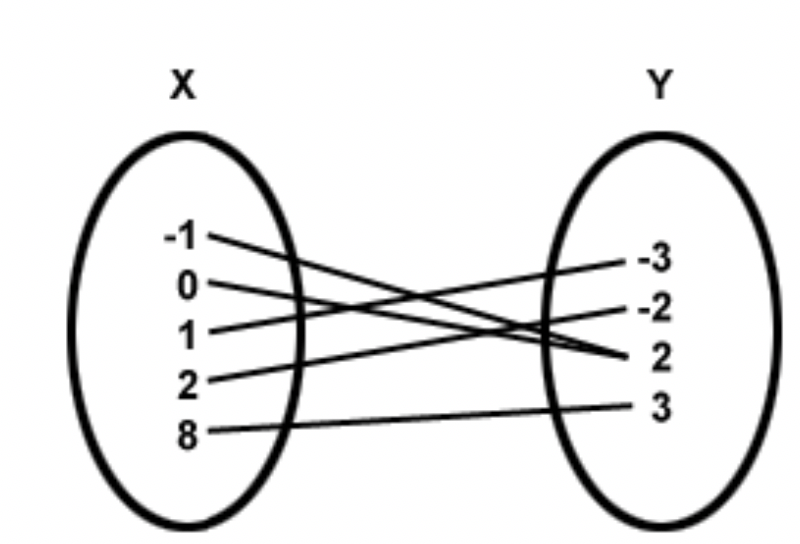
Yes
100
What is the value of the axis of symmetry?
y=1/2(x-1)^2-5
x=1
100
The cost, C, in dollars of operating a tile-cutting machine is modelled by
C(t)=2.2t^2-66t+655
where t represents the number of minutes the machine is run.
Will the optimal value of running the machine be a maximum or a minimum?
Minimum
100
A ball is thrown in the air from a cliff and its path is modelled by:
h(t)=-16t^2+48t+160
What is the initial height of the ball?
160m
100
Will the optimal value be a maximum or minimum?
y=-4(x+5)^2+7
Maximum
100
Set-up the problem:
The product of two consecutive integers is 420.
420=x(x+1)
200
Is the relation a function?
{(0,-3), (1,4), (-2,5), (0,2)}
NO
200
Solve for the roots:
x^2-6x+8=0
(4,0), (2,0)
200
The cost, C, in dollars of operating a tile-cutting machine is modelled by
C(t)=2.2t^2-66t+655
where t represents the number of minutes the machine is run.
How much does it cost to run the machine for 5 minutes?
$380
200
A ball is thrown in the air from a cliff and its path is modelled by:
h(t)=-16t^2+48t+160
What is the height of the ball after 4 seconds?
96 meters
200
What feature can you determine from looking at an equation in standard from?
the y-intercept
y=ax^2+bx+c; (0,c)
200
A rocket is launched and its height in meters after t seconds is given by
h=-1/2t^2+3t+45
After how many seconds did the rocket reach its maximum height?
3 seconds
300
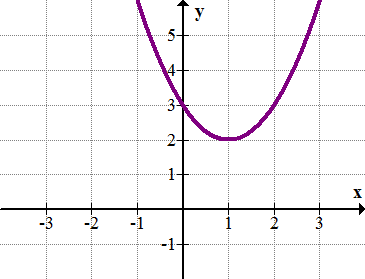State the Range:
R={yERR|y>=2}
300
State the nature of the roots of:
y=2x^2-7x+3
Two real roots
300
The cost, C, in dollars of operating a tile-cutting machine is modelled by
C(t)=2.2t^2-66t+655
where t represents the number of minutes the machine is run.
How long must the machine be running for the operating costs to be at a minimum?
15 minutes
300
A ball is thrown in the air from a cliff and its path is modelled by:
h(t)=-16t^2+48t+160
When does the ball hit the ground?
after 5 seconds
300
What is the quadratic formula?
x=(-b+-\sqrt(b^2-4ac))/(2a)
300
The length of a rectangular flower garden is 5 ft more than its width. If the area of the garden is 104 ft2, find the dimensions of the flower garden.
8ft by 13ft
400
State the Domain: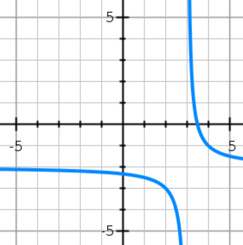
D={xERR|x!=3}
400
What is the optimal value of:
BONUS: State if it is a maximum or minimum value
y=4x^2-24x+40
Optimal value is 4.
It is a minimum value
400
The cost, C, in dollars of operating a tile-cutting machine is modelled by
C(t)=2.2t^2-66t+655
where t represents the number of minutes the machine is run.
What is the minimum operating cost?
$160
400
A ball is thrown in the air from a cliff and its path is modelled by:
h(t)=-16t^2+48t+160
At what time(s) is the ball at 192m?
1 and 2 seconds
400
Write
y=6x^2+12x+13
in vertex form
y=6(x+1)^2+7
400
The path of a skydiver’s jump out of an airplane can be modelled by
h(t)=5500-5t^2
where h represents the diver’s altitude in meters above the ground after t seconds of jumping out the plane.
If the diver opens his parachute at 1000m, how long did they free-fall?
30 seconds
500
State Domain and Range:
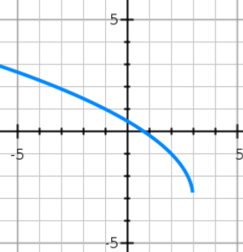
D={xeRR|x>=3}, R={yERR|y>=-3}
500
Solve for the roots:
6x^2+5x-6=0
x=-3/2, 2/3
500
The cost, C, in dollars of operating a tile-cutting machine is modelled by
C(t)=2.2t^2-66t+655
where t represents the number of minutes the machine is run.
How long has the machine been running if the cost is $255?
After 8.4 minutes or 21.6 minutes.
500
A ball is thrown in the air from a cliff and its path is modelled by:
h(t)=-16t^2+48t+160
What is the maximum height the ball reached?
196 meters after 1.5 seconds
500
State the vertex of:
y=-3x^2+18x-20
Vertex:
(3,7)
y=-3(x-3)^2+7
500
The length of a photograph is 1 cm less than twice the width. The area is 45cm2. Find the dimensions of the photograph.
5cm by 9cm