Domain & Range
Roots
Optimal Value
A ball is thrown...
Forms of a quadratic
Word problems
The cost to run a machine..
100
Is the following relation a function?
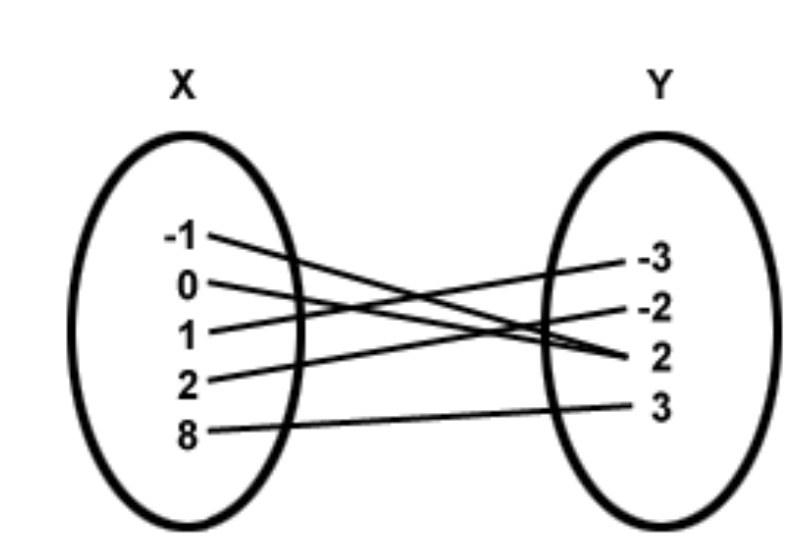
Yes
100
Solve for the roots:
6x^2+5x-6=0
(-3/2,0), (2/3,0)
100
What is the optimal value? Will it be a maximum or minimum?
y=-4(x+5)^2+7
Optimal Value is 7.
It is a maximum
100
A ball is thrown in the air from a cliff and its path is modelled by:
h(t)=-16t^2+48t+160
What is the height of the ball after 4 seconds?
96m
100
What feature can you determine from looking at an equation in standard from?
the y-intercept
y=ax^2+bx+c; (0,c)
100
The length of a rectangular flower garden is 5 ft more than its width. If the area of the garden is 104 ft2, find the dimensions of the flower garden.
8ft by 13ft
100
The cost, C, in dollars of operating a tile-cutting machine is modelled by
C(t)=2.2t^2-66t+655
where t represents the number of minutes the machine is run.
How much does it cost to run the machine for 5 minutes?
$380
200
State the Domain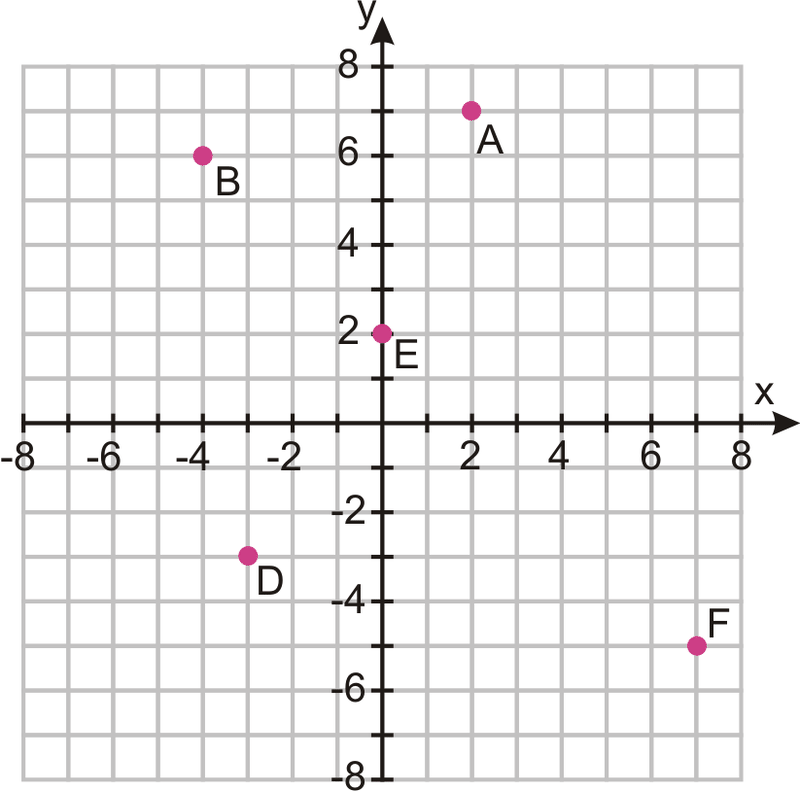
D={-4,-3,0,2,7}
200
State the nature of the roots of:
y=2x^2-7x+3
Two distinct real roots
200
A rocket is launched and its height in meters after t seconds is given by
h=-1/2t^2+3t+45
After how many seconds did the rocket reach its maximum height?
3 seconds
200
A ball is thrown in the air from a cliff and its path is modelled by:
h(t)=-16t^2+48t+160
When does the ball hit the ground?
5 seconds
200
Write
y=6x^2+12x+13
in vertex form
y=6(x+1)^2+7
200
The revenue for the school play is given by:
R(x)=-50x^2+300x
where “x” is the ticket price in dollars. The cost to produce the play is given by:
C(x)=600-50x
Determine the ticket price that will allow Script & Cue to break even.
$3 and $4
200
The cost, C, in dollars of operating a tile-cutting machine is modelled by
C(t)=2.2t^2-66t+655
where t represents the number of minutes the machine is run.
How long must the machine be running for the operating costs to be at a minimum?
15 minutes
300
State the Range: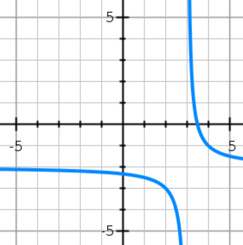
D={yERR|y!=-2}
300
For what value of k does the equation have two distinct real roots?
2x^2+6x+9k=0
k<1/2
300
Randy is building a fence at the side of his warehouse. He has 120m of fencing to work with and is using the side of the warehouse as one side of the rectangular fenced area. What are the dimensions of the maximum area that Randy can enclose?
30m by 60m
300
A ball is thrown in the air from a cliff and its path is modelled by:
h(t)=-16t^2+48t+160
At what time(s) is the ball at 192m?
1 and 2 seconds
300
Write the equation in factored form for a quadratic with roots 4, -2
and passes through the point
(0,-1)
y=1/8(x-4)(x+2)
300
The dimensions of a rectangular garden were 4 m by 5m. If each dimension was increased by the same amount, the area of the new garden is 56 m2. Find the amount each side of the garden was increased by.
3m
300
The cost, C, in dollars of operating a tile-cutting machine is modelled by
C(t)=2.2t^2-66t+655
where t represents the number of minutes the machine is run.
What is the minimum operating cost?
$160
400
State Domain and Range:
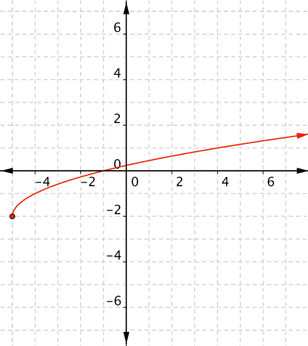
D={xERR|x>=-5}, R={yERR|y>=-2}
400
Find the exact roots of
y=9x^2+4x-16
x=(-2+-2\sqrt37)/9
400
Last year, the Musical tickets were sold for $11 each and 400 people attend. It have been determined that an increase of $1 in ticket price would cause a decrease in attendance of 20 people. What ticket price would maximize revenue?
$15.50
400
A ball is thrown in the air from a cliff and its path is modelled by:
h(t)=-16t^2+48t+160
What is the maximum height the ball reached?
196 meters after 1.5 seconds
400
Write the equation in, standard form, of a quadratic that has a vertex of (-3,2) and has a y-intercept of 5.
y=x^2+6x+15
[y=1/3(x+3)^2+2]
400
A movie stunt man jumped from the CN Tower and fell freely for several seconds before releasing his parachute. His height, h, in metres, t second after jumping is given by:
h=-4.9t^2+t+350
before he released his parachute, and
h=-4t+141
after he released his parachute.
How high was he when he released his parachute?
112.6m
400
The cost, C, in dollars of operating a tile-cutting machine is modelled by
C(t)=2.2t^2-66t+655
where t represents the number of minutes the machine is run.
How long has the machine been running if the cost is $255?
After 8.4 minutes or 21.6 minutes.