Properties 1
Properties 2
Always, Sometimes, or Never
Finding Angle Measures
Random Questions
100
What are the 3 properties of a quadrilateral?
- 4 sides
- 4 angles
- Interior angles add up to 360
100
Which quadrilateral has 4 congruent angles but not always 4 congruent sides?
Rectangle
100
A rectangle is ___________ a square
Sometimes
100
ABCD is a parallelogram and m<C=120. Find the m<EDF.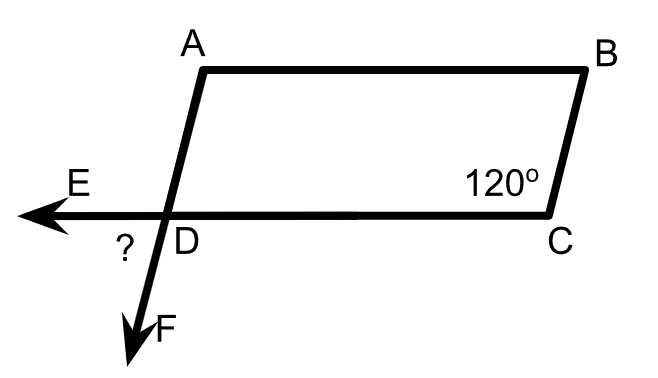
60
100
What is the Pythagorean Theorem?
a^2+b^2=c^2
200
What quadrilateral has 4 congruent sides and 4 congruent angles?
Square
200
Name a quadrilateral that always has two sets of opposite sides parallel.
Parallelogram, Rectangle, Rhombus, or Square
200
A parallelogram is ___________ a trapezoid
Always
200
Rhombus ABCD and diagonal AC are drawn. If m<BAC=64, what is the m<BCD?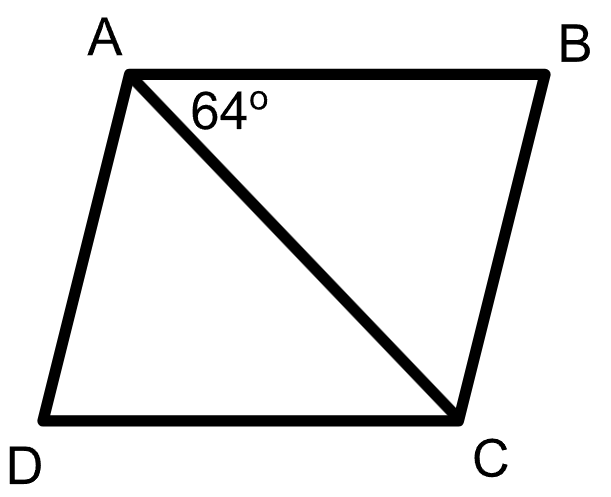
128
200
For a coordinate geometry proof, what is one method you can use to find a slope of a segment (not a vertical or horizontal segment)
- Rise over Run
- Slope formula
300
Which quadrilateral (besides a square) has perpendicular diagonals?
Rhombus
300
Name a property of a trapezoid
- At least one pair of parallel lines
- Consecutive angles whose common side is a leg are supplements
- Any property of a quadrilateral
300
A rhombus __________ has supplementary diagonals
Never
300
Parallelogram ABCD is drawn where m<A=(2x+10) and m<B=3x. Find the m<D.
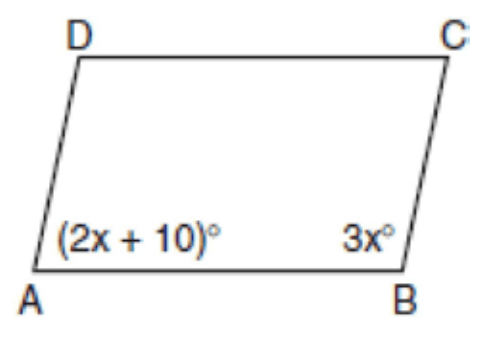
102
300
An isosceles trapezoid is drawn with a midsegment. Find the value of x.
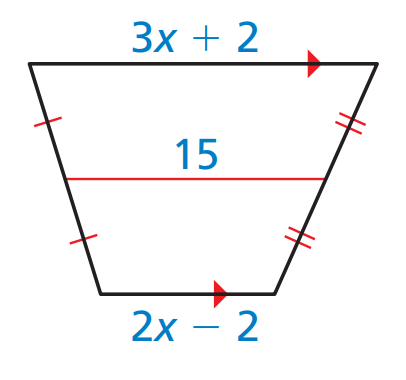
x=6
400
Which two quadrilaterals (besides a square) always have congruent diagonals?
Rectangle and Isosceles Trapezoid
400
Which quadrilateral (besides a square) has diagonals bisecting the angles?
Rhombus
400
A rectangle __________ has consecutive sides perpendicular
Always
400
Parallelogram FRED where AF=DF and m<R=124. What is the m<AFD?
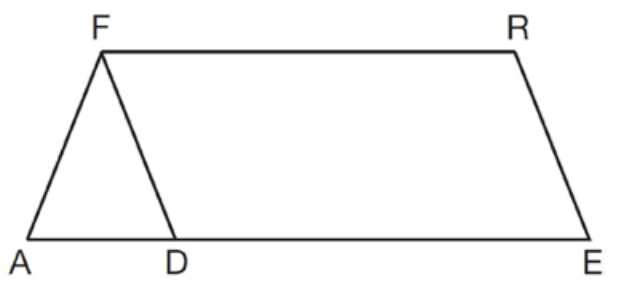
68
400
For a coordinate geometry proof, what is one method you can use to find a side length (not a vertical or horizontal side)
- Pythagorean Theorem
- Distance Formula
500
What are the 6 properties of a parallelogram (that are not always true of a trapezoid).
- Opposite sides are parallel
- Opposite sides are congruent
- Opposite angles are congruent
- Diagonals bisect each other (segments)
- Consecutive angles are supplementary
- One pair of opposite sides are congruent and parallel
500
What are the 4 properties of an isosceles trapezoid (that are not always true of a trapezoid)
- Legs are congruent
- Two sets of congruent base angles
- Opposite angles are supplementary
- Diagonals are congruent
500
A rhombus is __________ a rectangle
Sometimes
500
Rhombus ABCD is drawn with diagonals AC and DB intersecting at E. If m<ABE=67, what is the m<AED?
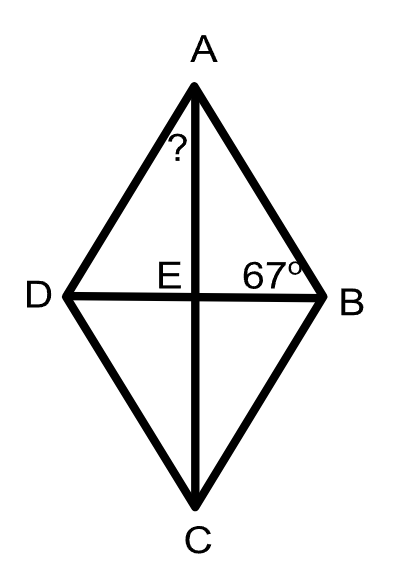
23
500
Segment AB has coordinates A(-2,1) and B(4,9). What is the length of AB?
10