If a point is on the perpendicular bisector of a segment, then it is ________________ to the endpoints of that segment.
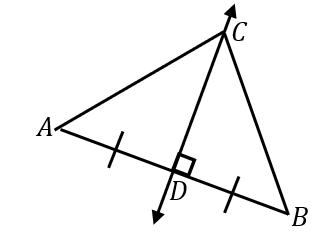
equidistant
The circumcenter is the point of concurrency of the ______________________________.
The circumcenter is equidistant from the _____________ of a triangle.
perpendicular bisectors ; angles
If a point is on the angle bisector of an angle, then the point is ________________ to the sides of the angle.
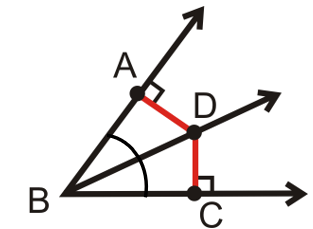
equidistant.
The incenter is the point of concurrency of the _______________________ of a triangle.
The incenter is equidistant from the ___________ of a triangle.
angle bisectors ; sides
Find AC.
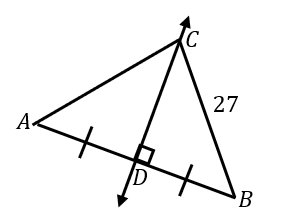
AC = 27
D is the circumcenter. Find UV, VD, and TD.
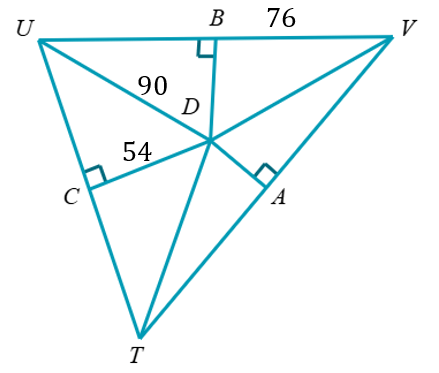
UV = 152
VD = 90
TD = 90
Find m∠CAD and m∠BAC.
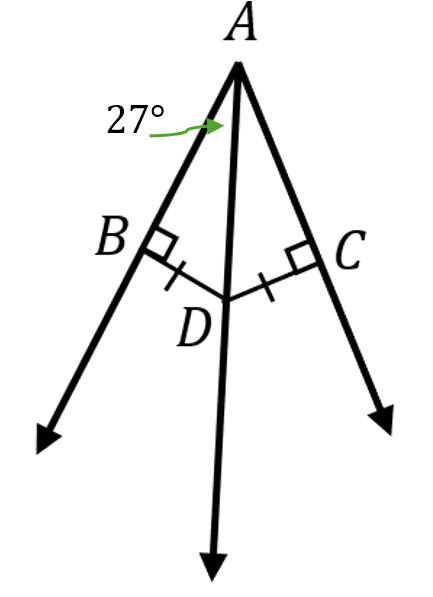
m∠CAD = 27°
m∠BAC = 54°
Suppose Q is the incenter. Find m∠NKQ, m∠NLQ, and m∠MJP.
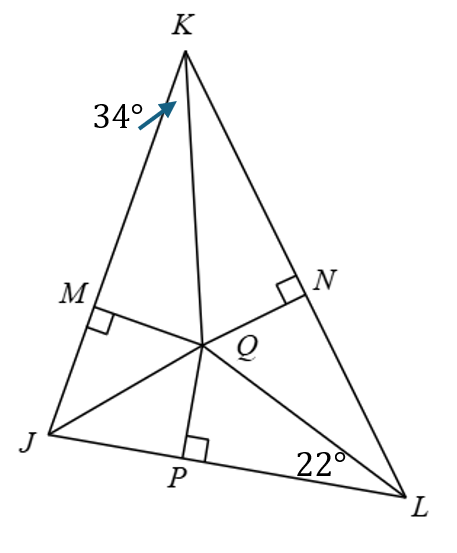
m∠NKQ = 34°
m∠NLQ = 22°
m∠MJP = 68°
Find XY.
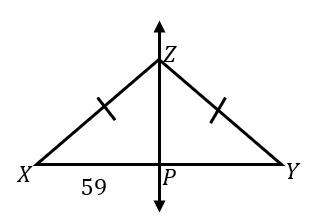
XY = 118
D is the circumcenter. Find TC and TU. 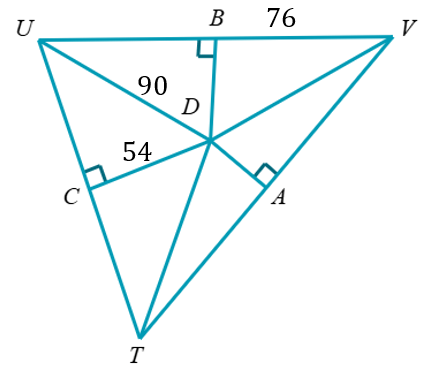
TC = 72
TU = 144
Find x.
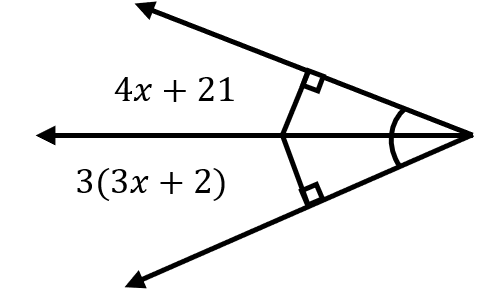
x = 3
Suppose Q is the incenter. Find PQ, NQ, and KN. Round answers to the nearest hundredth. 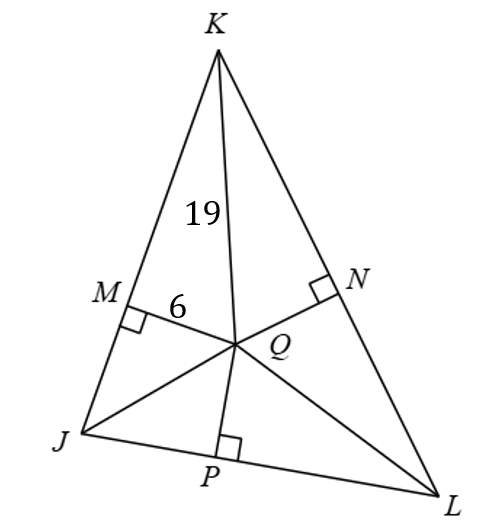
PQ = 6
NQ = 6
KN = 18.03
Find KL.

KL = 62
D is the circumcenter. If UD = 5(3x+4) and
VD = 10x+35, find TD.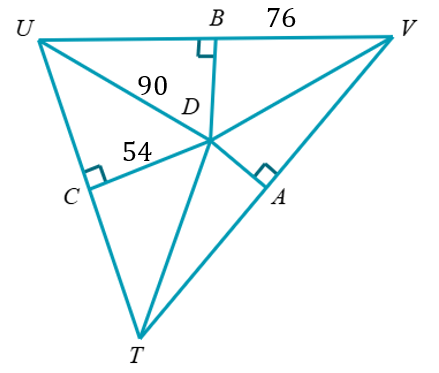
TD = 65
Find m∠UXW if m∠UVW = 112° .
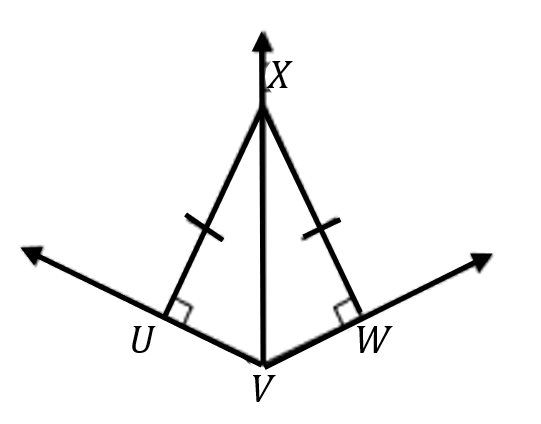
m∠UXW = 68°
Suppose S is the incenter. Find m∠PER and m∠QSR.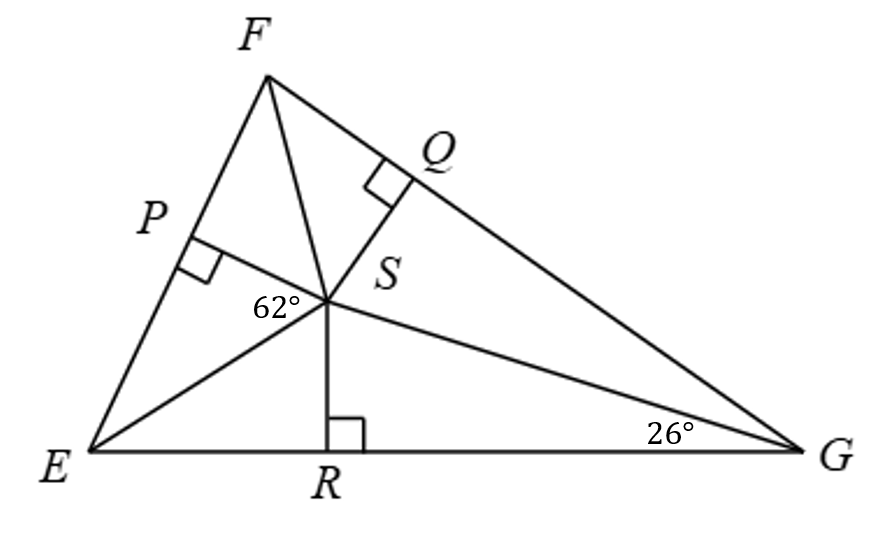
m∠PER = 56°
m∠QSR = 128°
If BD = 9x + 4, find BC and BD.
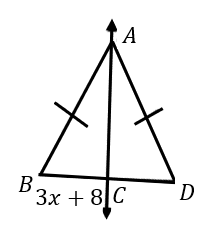
BC = 20
BD = 40
Suppose G is the circumcenter, EG = 36, AF = 52, and AG = 60. Find FG and EC. Round your answers to the nearest hundredth.
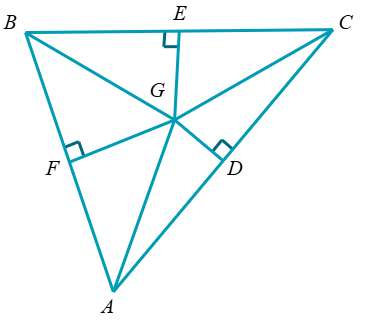
FG = 29.93
EC = 48
Find m∠ABC if m∠ABC = 7x - 11. 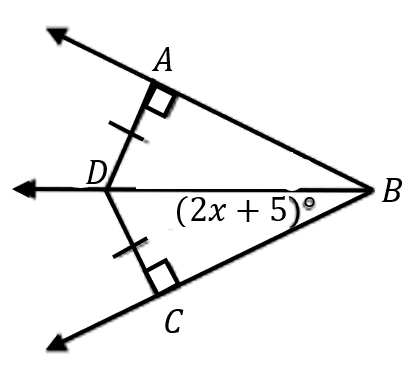
m∠ABC = 38°
Suppose S is the incenter. SP = 14, GS = 17, m∠PFQ = 94° , m∠RES = 22° . Find m∠REP, QG, and m∠RGS. Round your answers to the nearest hundredth.

m∠REP = 44°
QG = 9.64
m∠RGS = 21°