Arc Length/Equation of a Circle
Radians
Sector Area/Completing the square
Sector Area/Completing the Square ii
Arc Length/Equation of a Circle ii
100
The approximate arc length for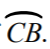
to the nearest hundreth
What is 7.68 inches?
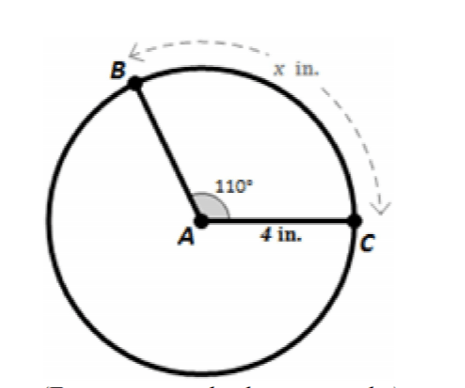
Arc Length =
(2pirTheta)/360
CB =
(2pi(4)(110))/360=(880pi)/360=(22pi)/9=7.68
100
Converted to radians
What is
pi/12?
100
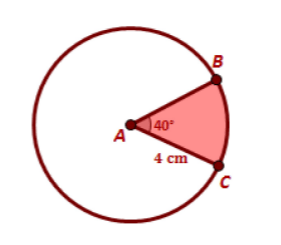
The sector area created by a circle with a radius of 4 cm and a central angle of 40°
What is
(16pi)/9 cm^3 or 5.6 cm^3?
Sector Area =
(pi(4^2)(40))/360=(640pi)/360=(16pi)/9
100
The radius is 5 cm, and the arc measure is 120 degrees, the sector area is ________. (Round to the nearest tenth)
What is 26.2 cm2
100
The radius is 16 ft, and the arc measure is 45 degrees, the arc length is ________. (Round to the nearest tenth)
What is 12.6 ft.
200
The major arc length for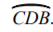 
to the nearest hundreth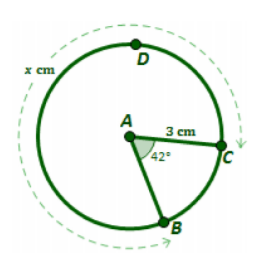
What is 16.65 centimeters?
Arc Length =
(2pirTheta)/360
CBD =
(2pi(3)(318))/360=(1908pi)/360=(53pi)/10=16.65
200
Converted to radians
What is
(2pi)/3?
200
Daily Double!!!
Solve for both solutions by completing the square:
a2 + 14a - 51 = 0
{3 and -17}
200
The radius is 6 m, and the arc measure is 90 degrees, the sector area is ________. (Round to the nearest tenth)
What is 28.3 m2
200
The radius is 9 m, and the arc measure is 120 degrees, the arc length is ________. (Round to the nearest tenth)
What is 18.9 m.
300
The minor arc length of
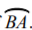in terms of pi
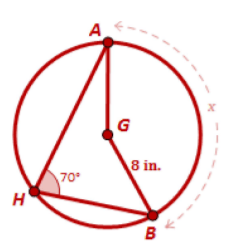
What is
(56pi)/9 cm?
Arc Length =
(2pirtheta)/360
Arc Length BA =
(2pi*8*140)/360=(2240pi)/360=(56pi)/9
300
Converted to degrees
What is 135°?
300
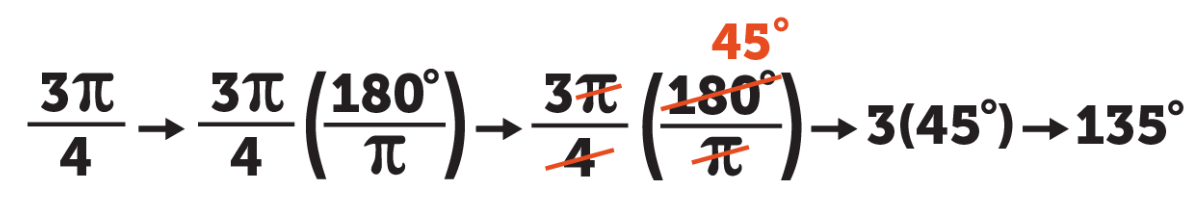
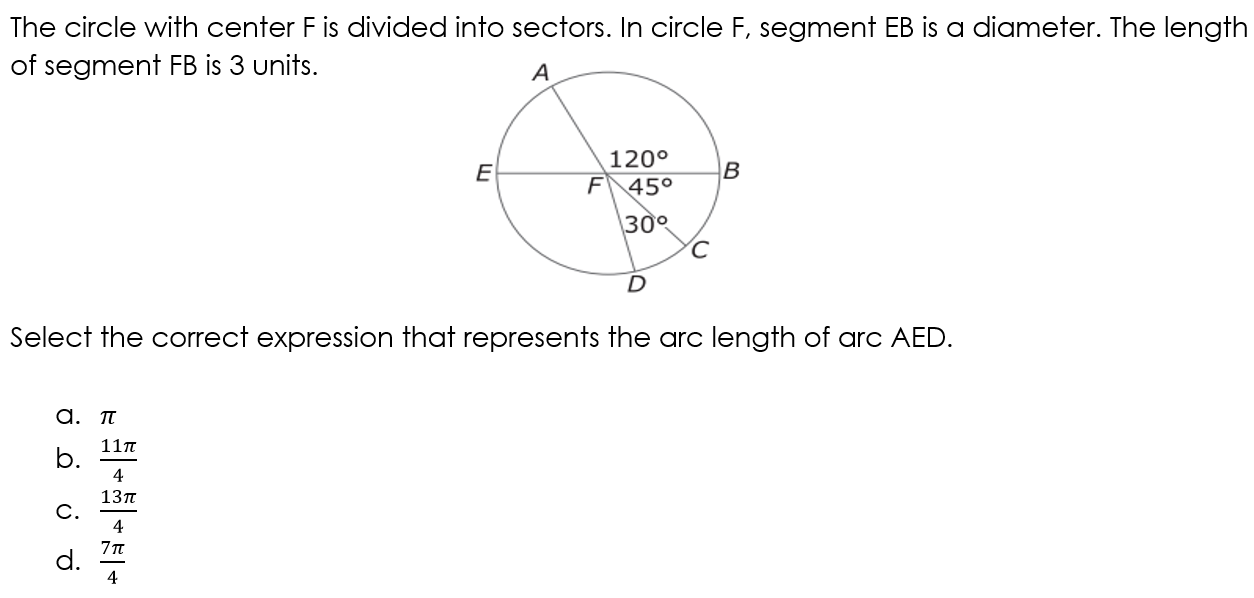
In circle O the radius is 7 cm. The area of the shaded sectors...
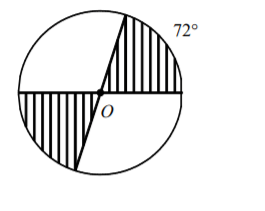
What is
(98pi)/5 = 61.6°?
Shaded Sector Area =
(pir^2Theta)/360=(pi(7^2)(144))/360=(7056pi)/360=(98pi)/5
300
The radius is 8 in, and the arc measure is 135 degrees, the sector area is ________. (Round to the nearest tenth)
What is 75.4 in2
300
Daily Double!!! Write the Circle Equation
2x2 + 2y2 + 28x − 24y + 8 = 0
What is (x + 7)2 + (y - 6)2 = 81
400
The approximate arc length of 
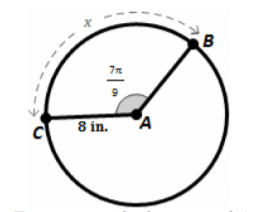
What is 19.55 cm?
When the central angle is given to you in radians you can use this arc length formula:
s=rtheta
Arc Length BC =
8*(7pi)/9=(56pi)/9=19.55
400
Converted to degrees
What is 480°?
400
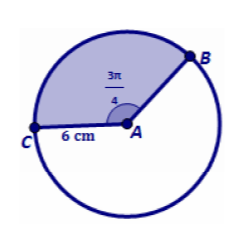
The sector area created by a circle with a radius of 6 cm and a central angle that measures
(3pi)/4 rads
What is
(27pi)/2 cm^3 or 42.4 cm^3?
Step 1: Convert Theta to Degrees
(3pi)/4*180/pi=540/4=135°
Step 2: Use Sector Area Formula
Sector Area =
(pi(6^2)(135))/360=(4860pi)/360=(27pi)/2
400
Daily Double!!! Solve by completing the square:
2a2 = -6 + 8a
What is {3 and 1}
400
The diameter is 3 m, and the arc measure is 160 degrees, the arc length is ________. (Round to the nearest tenth)
What is 4.2 m.
500
Write the equation of a circle with a diameter that has the ends (18, -13) and (4, -3)
(x - 11)2 +(y + 8)2 = 74
500
500
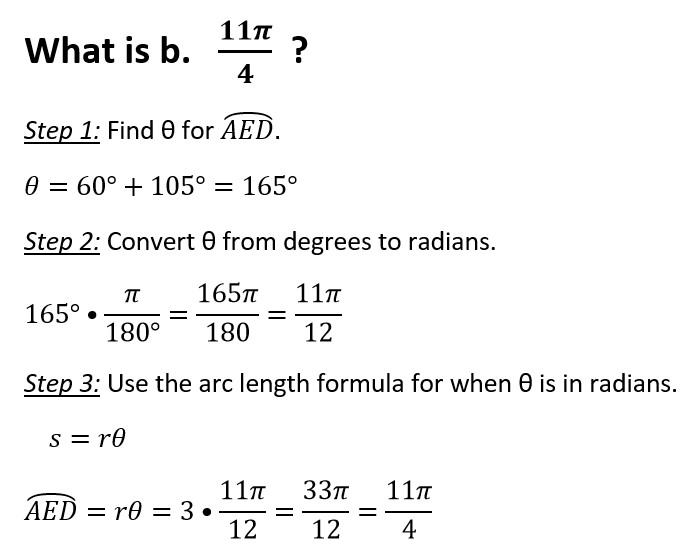
The approximate sector area defined by minor arc BA
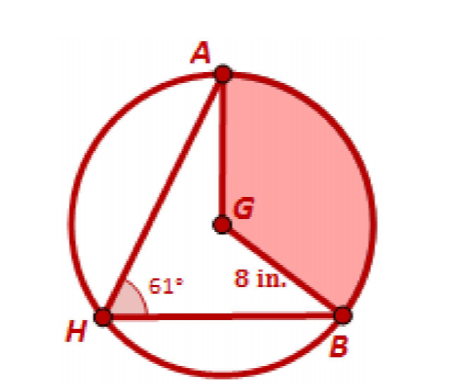
What is 68.1 in3?
Step 1: Find the central angle, Theta, for minor arc BA.
Theta=2*61=122°
Step 2: Use the Sector Area Formula.
Sector Area =
(pi(8^2)(122))/360=(7808pi)/360=(976pi)/4=68.1
500
The diameter is 40 cm, and the arc measure is
(5pi)/6
, the sector area is ________. (Round to the nearest tenth)
What is 523.6 cm2
500
The diameter is 16 units, and the arc measure is 90 degrees, the arc length is ________. (Round to the nearest tenth)
12.6 units