Ecuaciones cuadráticas
Formula general
Proporcionalidad
Congruencia y semejanza
Medidas de tendencia central
100
Menciona un ejemplo de factorización con números y otro con términos literales (letras).
Por ejemplo: 30=(6)(5) y a2=(a)(a).
100
¿Cuál es la formula general?
100
¿Cómo es el comportamiento entre el tipo de proporcionalidad directa e inversa?
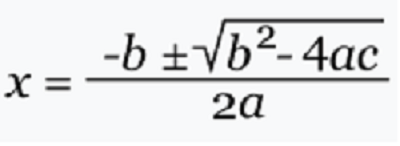
En proporcionalidad directa, si x aumenta, y también.
En proporcionalidad inversa, si x aumenta, y disminuye.
100
¿Cuándo podemos decir que dos triángulos son congruentes y cuándo son semejantes?
Dos triángulos son congruentes cuando tienen las medidas de sus ángulos correspondientes y lados correspondientes iguales.
Dos triángulos son semejantes si tienen sus ángulos correspondientes iguales pero sus lados correspondientes proporcionales.
100
Encuentra la mediana del siguiente conjunto de datos: 3,7,1,9,5.
1,3,5,7,9
Med=5
200
En la siguiente ecuación 3x2+6x=0 al resolver por factor común, los valores que satisfacen la ecuación son: x=0 y x=-2
Realiza la factorización de la ecuación para comprobarlo.
La factorización es 3x(x+2)=0
Por lo tanto x=0 y x=-2
200
¿Qué parte de la formula general nos permite saber si una ecuación cuadrática tiene soluciones y cuántas soluciones tiene?
El discriminante: Δ = b2-4ac
Un discriminante positivo indica que la cuadrática tiene dos soluciones reales distintas.
Un discriminante de cero indica que la cuadrática tiene una solución real repetida.
Un discriminante negativo indica que ninguna de las soluciones son números reales.
200
¿Cuál es la forma de la grafica para cada tipo de proporcionalidad?
200
Si dos triángulos tienen dos lados iguales y entre ellos un ángulo igual, ¿son congruentes? y si lo son ¿por cuál criterio?
Si, Criterio: LAL
200
Encuentra la moda del siguiente conjunto de datos: 4,8,6,8,10,4,5.
Mo=4 y 8
300
La ecuación x2+6x+9=0 es un trinomio cuadrado perfecto, ¿Qué característica de un trinomio cuadrado perfecto nos permite encontrar que la factorización de la ecuación es (x+3)2=0?
Un trinomio cuadrado perfecto se trata del cuadrado de la suma (o diferencia) de la raíz del primer y tercer término.
El segundo término es el doble de las raíces del primer y tercer término.
300
Un biólogo está modelando el crecimiento de una población de bacterias con la ecuación cuadrática: 4x2-12x+9=0, quiere saber cuantas soluciones tiene esta ecuación para predecir si la población alcanzará cierto nivel crítico en el tiempo. ¿Cuántas soluciones reales tiene este modelo?
Δ = b2-4ac
Δ =(-12)2 - 4(4)(9)= 144 - 144 = 0
La ecuación tiene una única solución real.
300
Marcos sale diariamente con su bicicleta y recorre todo el contorno del parque de su barrio. Él sabe que tarda aproximadamente 6 minutos en dar 3 vueltas al parque.
Si Marcos quiere dar 12 vueltas al parque,
¿Cuánto tiempo tardará?
Si y=kx entonces y=6, x=3
6=k(3)
k=2
y=2(12)
y=24
300
¿Cuál es el criterio de semejanza de los triángulos? Triángulo 1 tiene los siguientes lados:
- Lado 1: 5 cm
- Lado 2: 7 cm
- Ángulo entre los lados 1 y 2: 90º
Triángulo 2 tiene los siguientes lados:
- Lado 1: 10 cm
- Lado 2: 14 cm
- Ángulo entre los lados 1 y 2: 90º
Lado-Ángulo-Lado (LAL).
300
Encuentra la media del siguiente conjunto de datos: 15,20,25,10,30.
100/5=20
400
¿Cómo se puede saber que la siguiente ecuación x2-25=0 es un binomio conjugado y su factorización es (x-5)(x+5)=0?
Los binomios conjugados son pares de binomios que tienen los mismos términos, pero el signo que los une es diferente.
Al sacar la raíz cuadrada de cada término de la diferencia, obtienes los términos de los binomios conjugados.
400
Un objeto es lanzado desde una altura de 50m con una velocidad inicial de 10m/s. Su altura en función del tiempo t está dada por:
-5t2+10t+50=0
¿Cuánto tiempo tarda en tocar el suelo?
t1=−2.317
t2=4.317
El tiempo no puede ser negativo, por lo que tomamos la solución positiva:
t≈4.32 segundos
El objeto toca el suelo aproximadamente a los 4.32 segundos después de ser lanzado.
400
Un grupo de albañiles está construyendo un muro. Se sabe que si 4 albañiles tardan 15 días en terminarlo, ¿cuántos días tardará 6 albañiles en hacer el mismo trabajo, suponiendo que trabajan al mismo ritmo?
4/15 =6/x
60=6x
x=60/6
x=10
400
Un triángulo tiene lados de 6 cm, 8 cm y 10 cm. Otro triángulo tiene lados de 9 cm, 12 cm y 15 cm.
¿Cuál es la razón de semejanza entre los dos triángulos?
Razón de semejanza: 1.5
El segundo triángulo es 1.5 veces más grande que el primero.
400
Cierto o falso:
En el siguiente conjunto de datos 2,100,7,5,150,9 la media será mayor que la mediana.
Cierto
500
Al resolver la ecuación x2-7x+10=0 las raíces son x=5 y x=2, ¿Qué tipo de factorización se realiza para encontrar las raíces o soluciones?
Para factorizar esta ecuación se buscan dos números que al multiplicarse den el tercer término y al sumarse o restarse den como resultado el segundo término.
Se colocan como factores dos binomios con esos números.
500
Un terreno rectangular tiene un área de 120 m2. Su largo es de 2 metros más que su ancho. ¿Cuánto miden el largo y el ancho del terreno?
Sea x el ancho, entonces el largo es x+2. La ecuación es x(x+2)=120
x2+2x-120=0
x1=10
x2=-12
No hay magnitudes de longitud negativas entonces: x=10
Ancho=10m
Largo=12m
500
En un laboratorio se preparan dos soluciones químicas. La cantidad de un componente "A" en una solución es directamente proporcional a la cantidad de la solución, y la cantidad de un componente "B" es inversamente proporcional es al volumen de la solución. Se sabe que:
Para 50 litros de solución hay 5 gramos del componente "A".
Para 50 litros de solución hay 60 gramos del componente "B".
Si se prepara una nueva solución de 80 litros, ¿Cuántos gramos de los componentes "A" y "B" tendrá la nueva solución?
Componente "A"
5/50=gr/80
gr= (5*80)/50 =8
"A" = 8 gr
Componente "B"
(60*50)/(gr*80)=1
gr=(60*50)/80 =37.5
"B"= 37.5 gr
500
En el ΔPQR el ángulo P=40º, el ángulo Q=60º y el lado QR=12cm. En el triángulo ΔSTU los ángulos S=40º y T=60º y el lado TU=18cm. ¿Son los triángulos ΔPQR y ΔSTU semejantes?
Los triángulos tienen dos ángulos iguales cada uno, los triángulos son semejantes por el criterio AA.
500
En el siguiente conjunto de datos: 3,100,7,5,9,120,150 ¿la media será mayor que la mediana?
La media es 56.29 y la mediana es 9, entonces sí.