Resuelva la inecuación que se presenta. Reduce cualquier fracción a su mínima expresión. No redondees tu respuesta y no utilices fracciones mixtas. x+8<32
Escribe el resultado
representado en la recta numérica.

Si f(x)=x-8 calcula f(-5)
f(-5)=-13
De la ecuación 6m-7=n+5 escribe una función f(n) en términos de n
f(n)=(n+12)/6
P(t) modela el número de personas en la playa t horas después de la medianoche en un día específico. ¿Qué significa
P(11)=40?
A las 11 de la mañana hay 40 personas en la playa
Calcular el dominio, contradominio y rango de
f(x)=-8
D=mathbb{R}
C=mathbb{R}
R={-8}
8x-6\ge 1
en la recta numérica y en intervalos

(7/8,\infty)
Si f(x)=3x^2-7 calcular f(-4)
f(-4)=41
8(k-5)=3(m+1) escribe una función f(k) en términos de k
f(k)=(8k-43)/3
H(d) modela la altura máxima del balón de básquetbol (en metros) cuando es lanzado a una distancia horizontal de d metros de la canasta. ¿Qué significa H(3)<4 ?
La altura del balón es menor de 4 metros cuando es lanzado a 3 metros (de distancia horizontal) de la canasta.
Calcula el dominio, contradominio y rango de f(x)=x-9
D=mathbb{R}
C=mathbb{R}
R=mathbb{R}
5x>4x-4
Mostrar resultados en la recta numérica, en intervalos y en conjuntos.
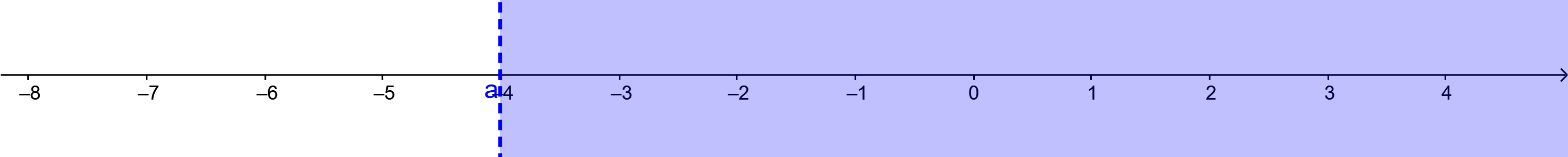
(-4,\infty)
{x\in\mathbb{R}|x>-4}
Si f(x)=4x+9 calcular f(k+2)
f(k+2)=4k+17
4(a+1)=(3b-5)/2 escribe una función f(a)
f(a)=(8a+13)/3
T(n) modela el número de inquilinos que viven en el piso n de la torre. ¿Qué significa T(5)>T(7) ?
En el piso 5 viven más inquilinos que en el piso 7.
Calcula el dominio, contradominio y rango de f(x)=x^2-5
D=mathbb{R}
C=mathbb{R}
R=[-5, infty)
Escribe el resultado representado en la recta numérica, en intervalos y en conjuntos
7x-8≤9x+2

[-5, \infty)
{x\in\mathbb{R}|x\geq -5}
f(x)=5x^2-4
calcular
f(n+8)
f(n+8)=5n^2+80n+316
4(a+1)=(3b+5)/2
escribe una función f(b) en término de b
f(b)=(3b-3)/8
D(t) modela la distancia que José recorrió (en kilómetros) después de caminar durante t horas. ¿Qué significa la proposición D(0.5)=2D(0.25) ?
La distancia que José recorrió en media hora es el doble de lo que camina en un cuarto de hora.
Calcula el dominio, contradominio y rango de f(x)=sqrt(12-x)
D=(infty,12]
C=mathbb{R}
R=[0,infty)
Escribe el resultado representado en la recta numérica, en intervalos y en conjuntos
-5x+7>3x-3

(-infty,5/4)
{x in mathbb{R}|x<5/4}
f(x)=4x^2-9x+1
calcular
f(h-3)
f(h-3)=4h^2-33h+64
(2(3u+5))/7=(-3(v-9))/4 escribe
f(v)
f(v)= (-21v+149)/24
H(t) modela la estatura de María José (en centímetros) cuando ella tenía t meses de edad. ¿Qué significa la proposición H(30)=H(25)+5 ?
Cuando María Josétenía 30 meses de edad, era 5 centímetros más alta que cuando tenía 25 meses.
Calcular el dominio, contradominio y rango de f(x)=(x+4)/(x+8)
D=mathbb{R}-{-8}
C=mathbb{R}
R=mathbb{R}-{1}