Function Notation
Function Notation
and Range
Functions
and Behavior of Functions
Is the following relation a function?
{(2, 4), (4, 4), (-1, 7)}
Yes
What is the domain of the following set?
{(2,4), (-4, 7), (-2, -1)}
{-4, -2, 2}
True or false:
The following function will have two solutions.
-|x+3|=9
False, it will have no solutions.
Are the following equivalent?
f(x)g(x) and f(g(x))
No, one is multiplication and the other is a composite function.
True or false:
The input values of the original function will be the input values of the inverse function.
False, the input values of the original function will be the output values of the inverse function.
True or false:
Transformation values on the inside of the parenthesis and attached to the x lead to horizontal transformations.
What is the average rate of change formula?
(\Deltay)/(\Deltax)
(f(b)-f(a))/(b-a)
Given the function
f(x)=sqrt(x+2
text{a. evaluate}\ f(7)
text{b. solve}\ f(x)=4
text{a.}\ +- 3
text{b.}\ x=14
What is the domain and range of the following function in interval notation?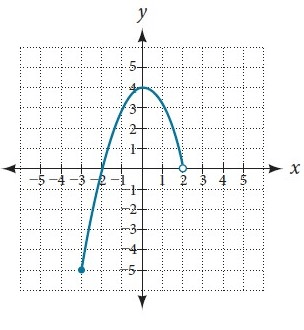
Domain
[-3, 2)
Range
[-5, 4]
True or False? Explain.
|X|>k\ text{is equivalent to} -k<X<k
|X|<k\ text{is equivalent to}\ X<-k or X>k
False, it should be
|X|<k\ text{is equivalent to} -k<X<k
|X|>k\ text{is equivalent to} X<-k or X>k
text{Using the image below evaluate}\ g(f(0)).
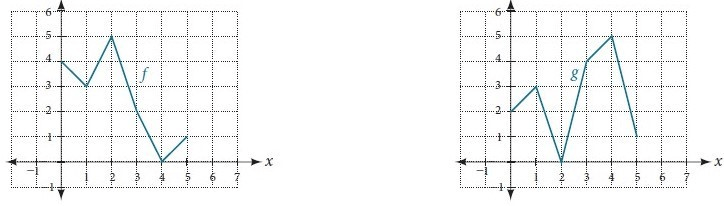
5
text{How do we algebraically verify two functions}\ ,f(x) and g(x),
text{are inverses of each other?}
We need to check if
f(g(x))=x and g(f(x))=x
Write an equation for the graphed function below by using transformations of the graph of one of the toolkit functions.
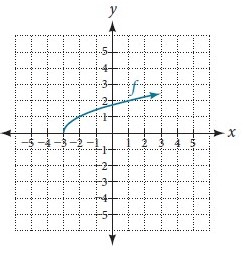
f(x)=sqrt(x+3
True or False:
text{The following function is increasing on the interval}\ [1, oo).
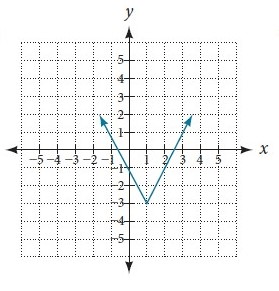
text{False, the function is increasing on the interval}\ (1, oo).
Is the following function one-to-one? Explain.
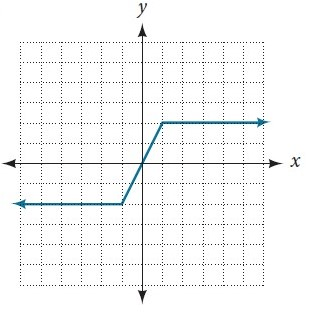
No, because it fails the horizontal line test.
Find the domain of the following function in interval notation:
(2x+1)/sqrt(5-x
(-oo, 5)
Solve the following equation.
3|x+1|-4=5
x=2 or x=-4
text{Given}\ f(x)=2x^2+1 and g(x)=3x-5, text{find the following:}
f(g(2))
3
Using the graph below, evaluate
f^-1(0)
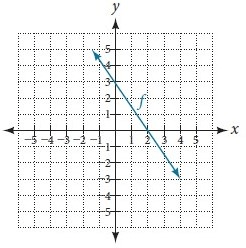
2
For the following, describe how the formula is a transformation of a toolkit function:
f(x)=sqrt(-2x+4
Horizontal reflection across the y-axis, horizontal compression by a factor of 1/2, and shifted right by 2 units.
For the following graph, identity all absolute extrema.
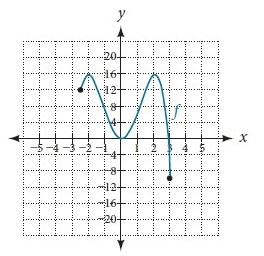
Absolute max is 16 when x = -2 and x = 2 (2, 16) and (-2,16)
Absolute min is -10 when x=3 (3, -10)
Consider the relationship
3r+2t=18
Write the relationship as a function
r=f(t)
r=(18-2t)/3
r=-2/3t+6
Does the following graph correspond to the piecewise function? Explain.
f(x)={(x^2,if x<=1),(3,if 1<x<=2):}`

No, we do not want to include the point (1, 3), so it should be an open circle.
Solve the following inequality and write your answer in interval notation.
|3x-4|<=8
[-4/3, 4]
text{Write}\ f(x)=|x^2+7|\ text{as the composition of two functions,}
h(x)!=x and g(x)!=x text{, such that}\ f(x)=h(g(x)).
g(x)=x^2+7 and h(x)=|x|
or
g(x)=x^2 and h(x)=|x+7|
Find the inverse of the following function:
f(x)=3/(x-2)
f^-1(x)=3/y+2
Write a formula for the function that results when the graph of the toolkit function is transformed as described:
text{The graph of}\ f(x)=1/x^2 text{is vertically compressed by a factor of}\ 1/3
text{, then shifted to the left 2 units and down 3 units.}
1/(3(x+2)^2)-3
For the following, find the average rate of change on the interval specified.
h(x)=x^2\ text{on}\ [1,5]
6