Define function
A relation that assigns has no more than one output for each input
Evaluate f(x)=–3x + 1 when x=2
What is f(2) = –5
What is f(–1)?

f(–1) = 3
Where is the following graph positive?
–2 < x < 2
Is the following a function?
{(2, 3), (4, 5), (–2, 6)}
Yes because x does not repeat
Define domain
All possible input or x values of a function
Find f(x) for x = –2 from the graph below

f(–2) = 1
Given f(x) = –3x – 10 find the input for f(x) = 20
x = –10
What is the x-intercept and y-intercept of this graph?

x-intercept: x = 3
y-intercept: y = –3
Is it a function?

No because it fails the vertical line test
Define range
All possible output or y values of a function
Evaluate f(x)= x2 + 4 when x=6
f(6) = 40
What are all inputs for this graph for f(x) = –4

x = 1 and x = –2
Where is this function increasing?

–2 < x < 0
Does the table represent a function?

Yes because x does not repeat
Define zero
An input value of a function that make the function equal to zero OR where the function crosses the x-axis
Given the piecewise function below, find f(7)

f(7) = 3
Given f(x) = 3x + 1
Find g(2) if g(x) = 4f(x) - 15
(hint: find g(x) first)
g(x) = 12x - 11
g(2) = 13
What is the maximum and minimum of this function?

Maximum: y = 5
Minimum: y = –6
Does this mapping represent a function?

No because –8 has two outputs
Define positive
Where the graph of a function is above the x-axis
Given the piecewise function below, what is f(2)?

f(2) = 1
What are the zeros of this graph?
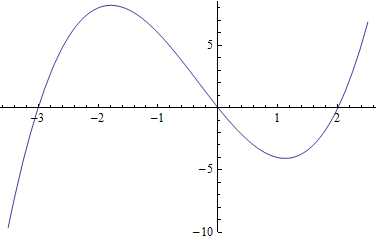
x = –3
x = 0
x = 2
What is the domain and range of this graph?
Domain: –3 ≤ x ≤ 2
Range: –2 ≤ y ≤ 3
Is it a function?

Yes because it passes the Vertical Line Test

