The "i's" have it!
Quadratic Equations
Quadratic Graphs
Power Functions
Polynomials
100
Simplify:
(2-i) + (4-2i)
6-3i
100
f(x)=-x2+4x-6, write in vertex form.
f(x)=-(x-2)2-2
100
Find the domain and range in interval notation:
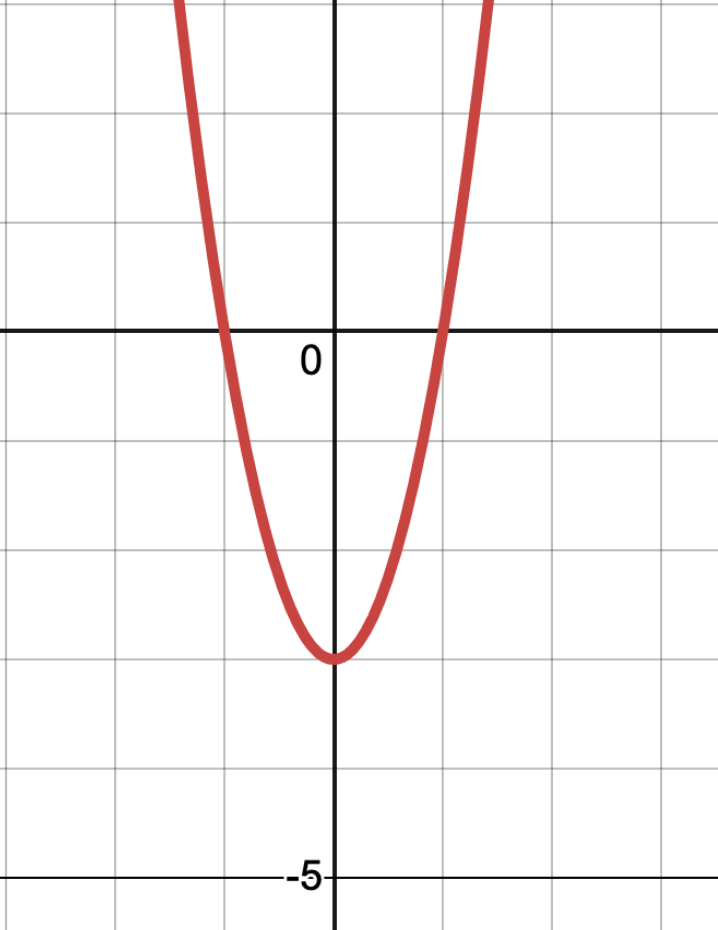
D: (-infinity, infinity)
R: [-3, infinity)
100
Is the following a power function:
2x^3(-3x^5)
yes
100
Is the following a polynomial function? Why or why not:
x^(2/3)(x^2+2)
No, 2/3 is a fractional exponent
200
Find the product:
(3-2i)(5+6i)
27+8i
200
Does the function have a max or min? What is it's value? Find the equation of the A.O.S.
f(x)=3x2+12x-5
minimum, value is -17, AOS: x=-2
200
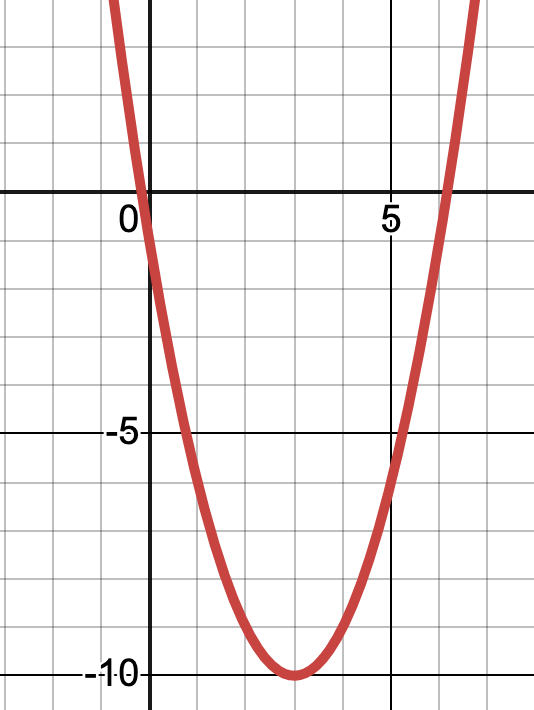
Sketch: f(x)=x2-6x-1. Show the y intercept also.
200
What is the end behavior?
-2x^3
up on the left, down on the right
200
Is this the graph of a polynomial function? Why/why not?
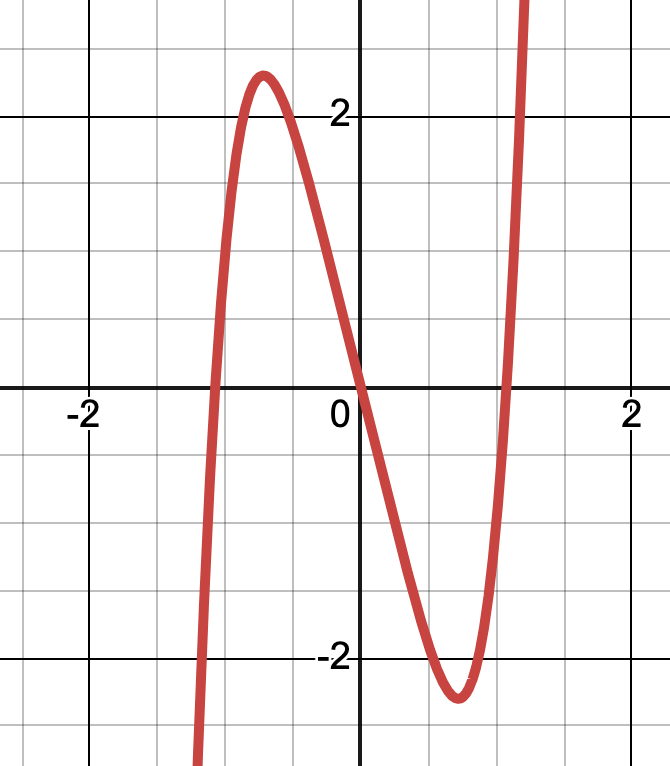
Yes, smooth and continuous
300
Simplify:
(4+i)/(3-i)
11/10+7/10i
300
Find the domain and range:
f(x)=3(x-4)2+1
D: (-infinity, infinity)
R: [1, infinity)
300
Find the x intercepts for
f(x)=x2-6x-1
x=
3+-sqrt10
300
What type of symmetry does a power function with an even exponent have?
y axis
300
End behavior?
f(x)=(2-x)^9
up on the left, down on the right
400
Simplify i41
i
400
Find the x intercepts:
f(x)= 3x2+2x-8
(4/3,0) and (-2,0)
400
Given the graph, write the equation in vertex form
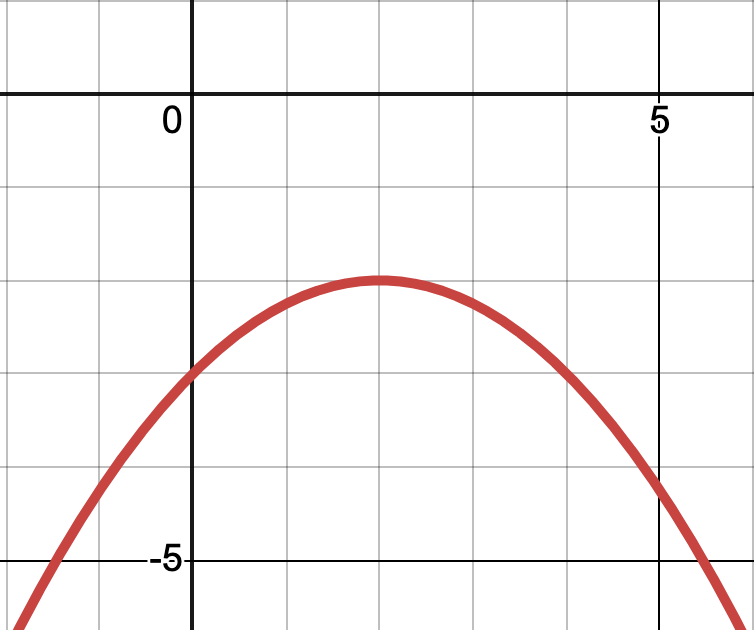
f(x)=
-1/4(x-2)^2-2
400
If f(-x)= -f(x), then the function is___________and has _____________symmetry.
odd, origin
400
Find the degree and the Lead Coefficient:
x^3(3x-1)^2
5, 9
500
f(x) = -x2+2x-1,
find f(2-2i)
3+4i
500
Given the info. below, find the equation in standard form: (h,k) = (-3,4) and (x,y) = (-2,1)
f(x)= -3x2-18x-23
500
Write the equation in standard form
f(x)=-1/4(x-2)^2-2
f(x)=
-1/4x^2+x-3
500
Over what interval is the power function decreasing:
-2x^5
(-infinity, infinity)
500
Find the x and y intercepts:
f(x)=4x(2x-5)(9x^2-1)
x: (0,0), (5/2,0), (1/3,0), (-1/3,0)
y: (0,0)