Trigonometric Functions and Their Inverses
The Law of Sines
The Law of Cosines
Trigonometric Identities, Formulas, and Equations
100
Evaluate cos(660^\circ) and sin(-30^\circ) .
cos(660^\circ)=1/2 and sin(-30^\circ)=-1/2
100
Find angle
∠B
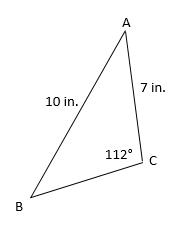
∠B=40.47^\circ
100
Find side CB using the Law of Cosines.
CB=21.6
100
Find all solutions of sqrt2cos\theta+1=0
\theta=(3pi)/4+2kpi
or
\theta=(5pi)/4+2kpi
200
Evaluate cos^{-1}(-1/2) , sin^{-1}(-2) , tan^{-sqrt3}(-1/2) and sin^{-1}(sqrt2/2) .
cos^{-1}(-1/2)=120^\circ
sin^{-1}(-2)=undefined
tan^{-1}(-sqrt3)=300^\circ=-60^\circ
sin^{-1}(sqrt2/2)=45^\circ
200
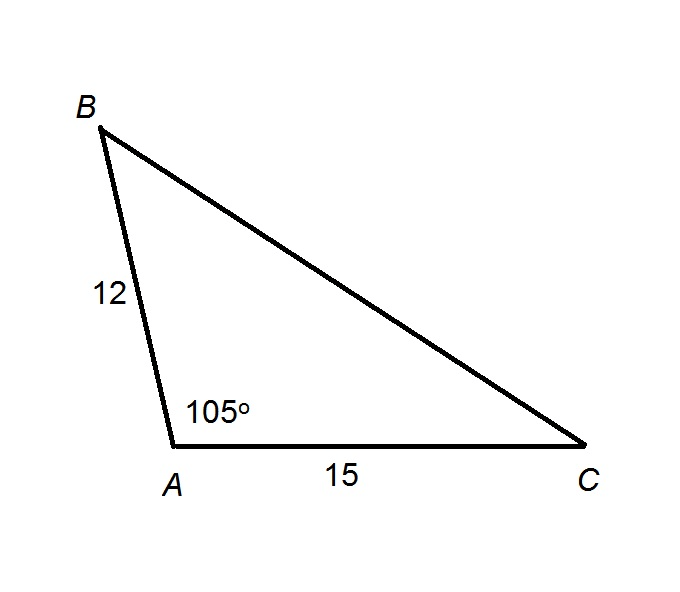
Find side AB using the Law of Sines.
AB=7.48 m.
200
Find the area of a triangle with sides of length 5, 6, and 8.
A=14.98
200
Simplify the following: sint/(1-cost)-csct
sint/(1-cost)-csct=cott
300
The base of a ladder is 6ft away from a building, and the angle formed by the ladder and the ground is 73^\circ . How high up the building does the ladder touch? How long is the ladder?
h=19.63
ft and
l=20.52
ft
300
Find all possible measures of ∠B if A=48^\circ, a=34, and b=39
∠B=58.21^\circ
or
∠B=121.79^\circ
300
In triangle ABC, a=9cm, b=10cm and c=13 cm. Find the size of angle
∠C
∠C=86.2^\circ
300
Simplify the following:
cos(x+y)+cos(x-y)
cos(x+y)+cos(x-y)=2cosxcosy
400
Find the 5 remaining trigonometric functions of \theta if cos\theta = -2/7 and tan\theta < 0 .
sin(theta)=(3sqrt5)/7
tan(theta)=-(3sqrt5)/2
csc(theta)=(7sqrt5)/15
sec(theta)=-7/2
cot(theta)=-(2sqrt5)/15
400
Solve the following triangle for all possible cases if A=86^\circ, a=15, and b=11
∠B=46.88^\circ
∠C=47.12^\circ
c=11.02
400
Find the area of a triangle with sides of length 8 and 14 and included angle
35^\circ
A=32.12
400
Find
sin(x/2)
cos(x/2)
tan(x/2)
if
cscx=3
and x is in the 2nd quadrant.
sin(x/2)=\sqrt{\frac{3+2\sqrt{2}}{6}}
cos(x/2)=-\sqrt{\frac{3-2\sqrt{2}}{6}}
tan(x/2)=3+2sqrt2
500
Find the area of a triangle with sides 10 and 22 and included angle 10^\circ .
A=19.1
500
In ΔABC, b=10 and ∠A=39^\circ .
What's a possible value for a that would produce two triangles?
Various correct answers.
500
A triangle has sides that measure 15, 17, and 30. What is the least measure of any of its angles?
19.1^\circ
500
Solve sin^2\theta =2sin\theta +3
\theta=(3pi)/2+2kpi